Bissectrice d'un triangle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
andrea73
- Membre Naturel
- Messages: 93
- Enregistré le: 18 Jan 2010, 17:15
-
 par andrea73 » 17 Nov 2010, 16:13
par andrea73 » 17 Nov 2010, 16:13
Bonjour,
Soit ABC un triangle dont tous les angles sont aigus et I le pied de la bissectrice de l'angle de sommet A dans ABC.
1.a. Montrer que aABI/aACI=BI/CI Et aABI et aACI désignent les aires des triangles ABI et ACI.
b.En déduire que I= bar[(B,aACI),(C,aABI)].
2.On note H et K les projetés orthogonaux de I sur (AB) et (AC). En calculant aABI et aACI d'une autre facon que dans la question précédente, montrer que
I=bar[(B,AC),(C,AB)]
3.Montrer que le barycentre du systeme[(A,BC),(B,AC),(C,AB)] est le centre du cercle inscrit dans le triangle ABC.
4.Le résultat précedent est-il encore valide si ABC possede un angle obtus(l'angle en B par exemple)?
Je suis en difficulté donc si vous pouviez m'aider se serai gentil. Merci

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 17 Nov 2010, 16:19
par Ericovitchi » 17 Nov 2010, 16:19
Ce sont des démonstrations très classiques, tu devrais chercher un peu sur internet :
exemple
-
andrea73
- Membre Naturel
- Messages: 93
- Enregistré le: 18 Jan 2010, 17:15
-
 par andrea73 » 17 Nov 2010, 16:30
par andrea73 » 17 Nov 2010, 16:30
J'ai regardé, mais je ne vois toujours pas comment faire pour la pemiere question, et je n'ai pas trouver deux facons differente de calculer l'air d'un triangle.
Merci de votre aide.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 17 Nov 2010, 16:37
par Ericovitchi » 17 Nov 2010, 16:37
les aires valent base x hauteur / 2 donc BI.AH/2 et IC.AH/2
leur quotient vaut donc bien BI/CI
Et puis après, les aires sont aussi AB.IH/2, etc...
-
andrea73
- Membre Naturel
- Messages: 93
- Enregistré le: 18 Jan 2010, 17:15
-
 par andrea73 » 17 Nov 2010, 16:53
par andrea73 » 17 Nov 2010, 16:53
C'est quoi H pour toi? Puisque si tu parle du H qui est dans la question 2, on a pas le droit de l'utiliser pour cet question.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 17 Nov 2010, 18:04
par Ericovitchi » 17 Nov 2010, 18:04
Ha oui, H c'était le pied de la hauteur donc appelle le autrement.
-
andrea73
- Membre Naturel
- Messages: 93
- Enregistré le: 18 Jan 2010, 17:15
-
 par andrea73 » 17 Nov 2010, 18:04
par andrea73 » 17 Nov 2010, 18:04
C'est bon pour la question 1 mais pour la question 2 je bloque?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 17 Nov 2010, 18:12
par Ericovitchi » 17 Nov 2010, 18:12
je t'ai déjà dit. tu dis que les aires c'est aussi AB.IH/2 et AC.IK/2 et donc que les quotient d'aire qui valaient BI/CI valent aussi AB/AC (puisque IH=IK puisque I est sur la bissectrice)
si M = bar[(B,AC),(C,AB)]
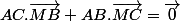
et en remplaçant AB/AC par BI/CI ça donne
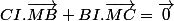
d'où on voit que le point M qui convient est I
-
andrea73
- Membre Naturel
- Messages: 93
- Enregistré le: 18 Jan 2010, 17:15
-
 par andrea73 » 17 Nov 2010, 18:21
par andrea73 » 17 Nov 2010, 18:21
Ouai, j'ai un peu pres compris, mais j'aurais juste besoin de ton aide pour la derniere question.
merci
-
andrea73
- Membre Naturel
- Messages: 93
- Enregistré le: 18 Jan 2010, 17:15
-
 par andrea73 » 18 Nov 2010, 16:36
par andrea73 » 18 Nov 2010, 16:36
Il faut que j'utilise quoi pour montrer que il y a un cercle inscrit et donc un barycentre?
merci beaucoup de votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
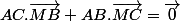 et en remplaçant AB/AC par BI/CI ça donne
et en remplaçant AB/AC par BI/CI ça donne 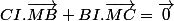 d'où on voit que le point M qui convient est I
d'où on voit que le point M qui convient est I