Borne sup borne inf.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Unknown-Girl
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Nov 2010, 11:38
-
 par Unknown-Girl » 16 Nov 2010, 11:59
par Unknown-Girl » 16 Nov 2010, 11:59
Salut tout le monde, y a une exercice que j'arrive pas à résoudre :mur:
1. Déterminer la borne supérieure et inférieure de l'ensemble :
A = {
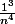
+
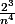
+ ... +
^3}{n^4})

}.
2. Pour tout entier n strictement supérieur à 0, on définit l'ensemble

= { k +
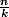
;
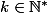
}.
Montrer que

admet une borne inférieure et que
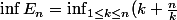)
.
3. Montrer que
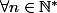
, inf
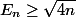
.
Merci d'avance.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 16 Nov 2010, 13:34
par Doraki » 16 Nov 2010, 13:34
Tu as essayé de simplifier l'expression an = 1^3/n^4 + 2^3/n^4 + ... + (n-1)^3/n^4 ?
ou de regarder si la suite (an) était monotone ?
Pour le reste, tu as essayé d'étudier la fonction k -> k+n/k ?
-
Unknown-Girl
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Nov 2010, 11:38
-
 par Unknown-Girl » 16 Nov 2010, 13:42
par Unknown-Girl » 16 Nov 2010, 13:42
Ouais pour la toute première question j'ai simplifié et j'ai trouvé à la fin que A={
^2)
} Par conséquent, tout x de A est compris entre 0 et
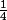
.
Puisque 0 appartient à A donc c l'inf, mais pour le sup j'essaie de trouver un

tel que
^2 \le \frac{1}{4})
mais j'obtiens que
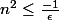
ce qui est impossible !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 16 Nov 2010, 13:51
par Doraki » 16 Nov 2010, 13:51
Là j'aimerais bien que tu m'expliques comment tu pars de 1/4 - ;) <= 1/4 (1-1/n)² pour arriver à n² <= -1/;).
Tu sais que dans l'inéquation de départ, quand n tend vers l'infni, à partir d'un moment elle doit être vraie, alors que dans ce que t'obtiens, tu l'as dit, c'est impossible.
Donc tu t'es forcément trompée quelquepart.
Par exemple, si ;) = 1/4, n'importe quel n doit convenir.
-
Unknown-Girl
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Nov 2010, 11:38
-
 par Unknown-Girl » 16 Nov 2010, 14:07
par Unknown-Girl » 16 Nov 2010, 14:07
On a
^2)
Donc
)
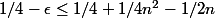
On peut négliger 1/2n parce que ça tend vers 0 à l'infini, et puis on simplifie par 1/4
On obtient donc -

inférieur à
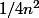
d'où

inférieur à -1 sur 4

-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 16 Nov 2010, 14:24
par Doraki » 16 Nov 2010, 14:24
Bon alors non seulement ton approximation est mauvaise, mais la fin de ton calcul est aussi mauvaise.
Admettons que je te laisse dire "1/4 - ;) <= 1/4(1+1/n²)".
Donc -;) <= 1/4n², oui.
Or, -;) est négatif, et 1/4n² est positif.
Donc n'importe quel n convient.
Tu ne peux pas dire que comme x -> 1/x est décroissante, ça équivaut à -1/;) >= 4n², parceque
x -> 1/x est décroissante sur R+* ou sur R-* mais pas sur les deux à la fois. C'est inutilisable quand les 2 trucs sont de signes différents. -1 <= 1, mais il est faux que -1 = 1/(-1) >= 1/1 = 1.
Par contre tu peux toujours multiplier par n² et diviser par (-;)) (négatif donc ça change le sens) pour obtenir n² >= -1/4;).
Mais en fait, comme 1/4 <= (1-2/n+1/n²) <= 1/4(1+1/n²), tu as élargi l'ensemble des solutions donc tu trouves des solutions à l'approximation qui ne sont pas des solutions du problème initial.
En fait, 1/n² est beaucoup beaucoup plus négligeable que 1/n.
Quand x tend vers 0, (1-x)² est approximé par 1-2x (-2 = la dérivée de la fonction en 0).
Donc quand on cherche un n tel que 1/4 - ;) <= 1/4(1-1/n)²,
il est raisonnable de chercher un n tel que 1/4 - ;) <= 1/4(1-2/n) < 1/4(1-1/n)²
Là on a de la chance, l'inégalité entre l'approximation et le truc initial est dans le bon sens.
Au lieu d'élargir l'ensemble des solutions, tu le réduis.
Pour être sûr de pouvoir encore trouver une solution en remplaçant (1-1/n)² par (1-2/n),
tu peux vérifier que quand n -> l'infini, 1/4(1-2/n) tend toujours vers 1/4, donc tu trouveras des solutions et tu peux continuer.
-
Unknown-Girl
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Nov 2010, 11:38
-
 par Unknown-Girl » 16 Nov 2010, 18:40
par Unknown-Girl » 16 Nov 2010, 18:40
Bon pour la toute première question c'est réglé, mais je me bloque dans les 2 questions qui suivent, et je vois pas le lien entres ces 2 questions et la première question de l'exo !!
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 19 Nov 2010, 00:06
par bentaarito » 19 Nov 2010, 00:06
bon pour la deux il suffit d'étudier le sens de variation de
=k+\frac nk)
tu dois trouver qu'elle admet un min absolue en
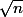
et donc t'auras même
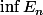
=
)
.
pour la trois remarque que
= 2\sqrt n)
.
-
Unknown-Girl
- Membre Naturel
- Messages: 12
- Enregistré le: 16 Nov 2010, 11:38
-
 par Unknown-Girl » 20 Nov 2010, 12:14
par Unknown-Girl » 20 Nov 2010, 12:14
J'ai étudié le sens de variation de
 = k + \frac{n}{k})
et j'ai trouvé qu'elle est décroissante de 0 à
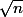
et croissante de
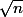
jusqu'à l'infini, avec
 = 2\sqrt n)
donc par conséquent on a
 = 2\sqrt n)
, mais là comment passer et conclure que
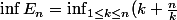)
?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Nov 2010, 16:12
par Doraki » 20 Nov 2010, 16:12
montre que pour tout k dans N* il existe k' dans {1...n} tel que (k+n/k) >= (k'+n/k')
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités