Equations différentielles

par **Antony67** » 15 Nov 2010, 18:19

Bonjour, je n'arrive pas à résoudre ces équations différentielles, pouvez-vous m'aider svp?

1) y' + 2y = 4x
2) y" + 2y' - 3y = e^(-2x)

Merci d'avance

par **Arnaud-29-31** » 15 Nov 2010, 18:51

Salut,

Tu bloques ou ? Tu as vu en cours comment résoudre ce genre d'équations ?

par **Antony67** » 15 Nov 2010, 19:16

je n'arrive pas à trouver les solutions particulières de y' +2y = 0

par **Arnaud-29-31** » 15 Nov 2010, 19:19

Tu as donc trouvé les solutions de l'équation homogène ?
Pour la solution particulière, on cherche tout simplement quelque chose de la forme f(x) = ax + b

par **Antony67** » 15 Nov 2010, 19:21

non justement, je n'arrive pas à résoudre y'+2y=0 pour trouver la solution générale

par **Antony67** » 15 Nov 2010, 19:27

Les solutions de y'+2y=0 sont bien g(x) = Ce-2x où C est une constante réelle?

par **kasmath** » 15 Nov 2010, 19:28

Antony67 a écrit:non justement, je n'arrive pas à résoudre y'+2y=0 pour trouver la solution générale

simple question de cours

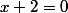
implique ou X=-2 c'est l'equation caractéristique de l'équation différentiel y'+2y=0et tu applique le cours

par **Arnaud-29-31** » 15 Nov 2010, 19:41

Antony67 a écrit:Les solutions de y'+2y=0 sont bien g(x) = Ce-2x où C est une constante réelle?

Oui c'est bien ça. Dans le cours tu dois avoir les solutions de y' + ay = 0 sont de la forme

par **Antony67** » 15 Nov 2010, 19:44

et pour trouver les solutions particulières je fais comment?

par **Arnaud-29-31** » 15 Nov 2010, 19:55

Tu cherche UNE solution particulière.
Lorsque que le second membre est un polynôme, on cherche un polynôme de même degré soit donc une solution particulière de la forme f(x) = ax+b

par **Antony67** » 15 Nov 2010, 20:00

ce qui donne a+2(ax+b)=4x donc a=2 et b=-1
et donc la solution générale c'est y=2x-1+Ke^{-2x} ?

par **Arnaud-29-31** » 15 Nov 2010, 20:14

Oui, ca a l'air pas mal.

Equations différentielles

Equations différentielles

Qui est en ligne