Calcul de Résidus

[Fløw]

Bonjour,
Petite question pour savoir si vous pouvez me dire si ce raisonnement est juste :
Étude des singularités :

Calcul des singularité :

On a donc 8 pôles simples pour cette fonction.
Calcul du résidu :
On pose : grâce à la formule => f(z) = u/v(z)
On a donc un résidu égal pour les 8 pôles simples étant de :


True or False ? Qu'en dites-vous ? :hum: :hein:

Merci d'avance

[Ben314]

Salut,

On a donc un résidu égal pour les 8 pôles simples étant de :


True or False ?

Ben, ça dépend un peu de la façon dont on interprète ta phrase qui est un peu incohérente :
Si on considère que tu as écrit :
"On a donc un résidu égal pour le pôle z=-1 : "
alors la réponse est "true"

Si on considère que tu as écrit :
"On a donc un résidu égal pour n'importe lequel des 8 pôles : "
alors la réponse est "false"...

[Fløw]

Et si on écrit plus généralement :

On peut écrire ça non ?
avec k variant de 0 à 7. On a donc un résidu k pour un kème pôle.

[Ben314]

Cette fois, c'est correct, mais, perso, j'écrirait uniquement que
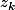
(vu que ) et je remplacerait pas le par exp(...) qui alourdit inutilement le résultat.

[Fløw]

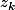
je remplacerait pas le par exp(...) qui alourdit inutilement le résultat.

C'est ce que j'aurais fais sur une copie d'exam aussi, mais j'voulais être sur de l'expression.

Ok Ok bah merci...Je crois que j'ai acquis à peu près les bases. . . .Un peu grâce à toi quand même. Merci ^^