Limite : Forme indéterminé

[Peter/seconde]

Bonjour,
Un exercice me demande : Étudiez la limite en -2 de f(x) =
J'ai donc fais :
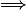
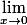
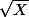
Quand x tend vers -2 et x 0) avec 0 > 0 de = 0 ( > 0)
Mais je n'arrive pas à enlever la forme indéterminé après, ce n'est pas un taux d'accroissement et on ne peut pas mettre une formule en facteur.
Merci de vos aides.

Au revoir.

[joseph]

Bjr

Multiplier les deux termes par le dénominateur
Simplifier ensuite par (x+2)

[Mortelune]

Bonjour, sinon tu peux factoriser ton dénominateur et voir ce que ça te simplifie :)

[Peter/seconde]

pour Joseph : J'ai multiplié comme tu m'as dis ça me donne : ce qui me donnerait donc comme limite 0 puisqu'on aura 0 en haut et 4 en bas.

pour Mortelune : Je ne comprends pas comment tu veux que je factorise la racine à part avec mais ça ne m'aiderait pas beaucoup.

[Mortelune]

x²-x-6=(x+2)(x-3)

[Peter/seconde]

Ah oui pardon, merci bien de cette correction j'ai pris (+x) lorsque j'ai factoriser.