Tribu atomique

[Aspx]

Bonjour,

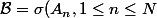Si on considère un ensemble et une partition de cet ensemble disons . On note . On dit alors que est atomique. Comment alors montrer que tout variable aléatoire -mesurable est constante sur chacun des ?

J'ai bien l'impression que si l'espace d'arrivée est séparé ça marche bien mais ma preuve par l'absurde ne donne rien pour l'instant...

Merci par avance!

[Ben314]

Salut,
Il faudrait que tu précise ce que tu entend par "variable" : clairement c'est une fonction dont l'ensemble de départ est Omega, mais quel est l'ensemble d'arrivé Omega' ?
à priori, j'aurais bien dit un espace mesuré quelconque, mais tu parle d'espace "séparé" ce qui semblerait vouloir dire que Omega' est un espace topologique (muni de la tribu engendrée par les ouverts ?)
Est tu sûr que le mot "variable" ne désigne pas une variable réelle ?

[Aspx]

Oubli : j'entendais évidemment variable aléatoire, ie -mesurable. L'espace d'arrivée est topologique et je parlais d'espace séparé car j'ai l'impression que la démonstration tient à ça, mais on peut se restreindre au cas métrique (où l'espace est forcément séparé) ou encore "pire" en prenant . Désolé pour les imprécisions, ainsi que pour avoir posté sur le mauvais forum... Si on pouvais me rediriger d'ailleurs :hein:

edit : j'ai modifié l'énoncé, la partition est finie

[Ben314]

Effectivement, si l'espace topo d'arrivé est muni de la topologie grossière, toute fonction "atterissant" dans E sera mesurable.
Bon aprés, dans le cas où E est séparé (il suffit même de supposer que les singletons sont fermés, ce qui est légèrement plus faible) le résultat parrait assez évident et il n'y a pas vraiment besoin d'absurde : La seule constatation à faire, c'est que les parties mesurables de Omega sont les réunions de certains Ai (et si I était infini dénombrable, cela ne changerais rien)

[Aspx]

En effet si on arrive à montrer que tout ensemble mesurable est réunion de certains Ai on a gagné. Déjà l'ensemble formé de toutes les réunions possibles des Ai forme une tribu grâce au fait que les Ai forment une partition de . C'est évidemment la plus petite tribu donc égale à .

Il suffirait ensuite de prendre l'image réciproque d'un singleton. Il se pourrait cependant que cela soit toujours l'ensemble vide... Sauf si on se limite à ImX, où X désigne la variable aléatoire en question. Ok! Merci bcp!

[Ben314]

...Il se pourrait cependant que cela soit toujours l'ensemble vide...

Si par exemple, au lieu de prendre un singleton "au pif" dans l'ensemble d'arrivé, tu part d'un a dans Ai et que tu considère le singleton {f(a)} de l'ensemble d'arrivé, ça ce passe tout de suite mieux...