Exercice sur les barycentres

[fabes]

bonsoir, j'aurais besoin d'aide pour un question sur les barycentres.

Determiner l'ensemble (H) des points de l'espace tels que:

(MA+2MB+MC).(MA-2MB+MC)=0

merci d'avance

[Ben314]

Salut
RAPPEL de ton cours (fonction vectorielle de leibnitz) :
Si sont des points d'un espace affine , des réels et si, pour tout de on pose alors
1) Si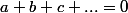 la fonction est constante.
2) Si alors il existe un unique point de (appellé barycentre de ) tel que, pour tout de , on ait

Résultat à savoir "par coeur" et il faut aussi savoir retrouver la preuve (de 2 lignes)

2 em "Rappel" : le produit scalaire de deux vecteurs est nul ssi ils sont orthogonaux.

[fabes]

dsl, j'avais oublié de dire que l'on nous a imposé un repère (A,AB,AD) avec K=AB^AD
et merci pour l'aide

[benekire2]

Oui, ça ne change rien au début , suit ben, il est de bons conseils :ptdr:

Ensuite tu caractérisera ton ensemble à l'aide de ton repère si ça te chante. Ou alors tu le fais version analytique, mais perso je trouve ça moins bien :lol3:

[flight]

sauf erreur l'ensenble des points cherchés est un cercle

[Actéon]

sauf erreur l'ensenble des points cherchés est un cercle

non attention ce n'est pas un cercle, justement car un des deux vecteurs est un peu particulier...