Terminale s complexes

[Madlord]

Bonsoir,
j'ai de nouveau u problème avec un exercice de complexe, en effet j'ai .

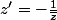
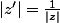
J'ai déja calculé que et que .

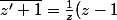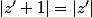
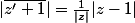
On me demande de prouver que et là je bloque, j'en suis arrivé à dire que je sens que je suis près du but mais j'ai beau me creuser la soupière je n'arrive pas au bon résultat.

[Sylviel]

dis comme ça ton résultat est faux : pour z=1, z'=-1 et 0 ne vaut pas 1...

[Madlord]

Il ne s'agit pas de Z' mais de |z'|, de son module.

[Sylviel]

oui et tu as essayé avec z' = -1 ?

[Madlord]

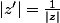
Je ne comprend pas là où tu veux en venir, il faut que je prouve l'égalité pour toute les valeurs de z et z'. Si je prend un nombre arbitraire pour une démonstration, il faut que je prouve pour l'infinité de nombre qu'il reste autant dire que je ne suis pas couché ... Je sens qu'il faut que je me serve du fait que et donc comment à partir de arriver à ?

[Madlord]

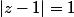
Bon, et bien le problème venait de moi, je n'avais pas vu que dans l'énnoncé il y avait et don lorsque je suis arrivé à j'aurais du simplifier par un et j'aurai trouvé la bonne réponse, parfois la résolution d'un exercice de maths c'est simple comme d'ouvrir les yeux.

[Sylviel]

Ce que je t'ai dit à plusieurs reprise c'est que ce que tu cherchais à démontrer était en général faux. z'=-1 était un contre-exemple, pour t'inviter à bien regarder ton énoncé !