Petit soucis en complexes !

[Mobster]

Bonsoir mes frayres :)
Je bloque sur un exo sûrement simple.
Soit a un complexe.
On considère (E) d'inconnue z (complexe) : [(1+iz)/(1-iz)]^4 = a.
1. On suppose que (E) a une solution réelle x, montrer que a est de module 1.
-> Ça, c'est fait !
2. Quelles sont les solutions de l'équation d'inconnue T (complexe) : T^4 = a ?
-> Là je bloque.
Je dis que, du coup, |T|^4 = 1, puis il faudrait que je fasse les racines quatrièmes de l'unité, mais on peut que dans les complexes non ? Et vu qu'un module est un réel.. Je bloque ^^"
Merci d'avance de votre aide ;D

[Nightmare]

Hello,

c'est presque ça, si on trouve les racines 4ème de l'unité (qui ne sont autre que 1, -1, i et -i, je te laisse le montrer facilement), tu conviendras que si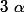 est une racine 4ème de a, toutes les solutions de l'équation 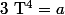sont . Du coup, il reste juste à trouver une racine 4ème de a, pour ça, on peut par exemple passer sous forme exponentielle...

[Mobster]

Hello, merci de ta réponse !
J'ecris T sous la forme r.e(i.tétha), donc le module de T vaut r.
J'ai donc r^4=1 à résoudre. Comme r est réel, je vois pas quoi mettre comme solution, je peux pas mettre les racines quatrièmes de l'unité vu que deux d'entre elles sont complexes ?
J'attends ta réponse avec impatience, merci d'avance !

[Mobster]

En fait je sais pas pourquoi je fais ma fixette sur le module de T.
En fait pour la racine quatrième de a, je trouve e(i.théta/4), où thêta est l'argument de a. Mais j'imagine que c'est pas ça ?

[Nightmare]

Si, c'est bien ça !

[Mobster]

Ah, ouf !
Donc je mets que les solutions sont z, -z, iz, -iz, ou alors il fait que je les recalcule ?
Merci encore !

[Mobster]

J'ai de nouveau besoin d'aide pour la suite.
Je dois ensuite exprimer les solutions z0 z1 z2 et z3 de (E) en fonction des solutions de l'équation T^4 = a.
Mais je vois pas trop quoi faire.
Résoudre (E) en mettant (1+iz0)/(1-iz0) = w0, puis faire de même avec w1, w2, w3, avec w la solution trouvée à l'équation T^4 = a ?

[Ben314]

J'ai de nouveau besoin d'aide pour la suite.
Je dois ensuite exprimer les solutions z0 z1 z2 et z3 de (E) en fonction des solutions de l'équation T^4 = a.
Mais je vois pas trop quoi faire.
Résoudre (E) en mettant (1+iz0)/(1-iz0) = w0, puis faire de même avec w1, w2, w3, avec w la solution trouvée à l'équation T^4 = a ?

Oui, c'est bien ça.