Démonstrations par récurrence !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mobster
- Membre Relatif
- Messages: 241
- Enregistré le: 29 Oct 2008, 20:42
-
 par Mobster » 03 Nov 2010, 17:13
par Mobster » 03 Nov 2010, 17:13
Bonsoir mes frayres !
Je dois démontrer ces deux égalités :
Quel que soit n de N, la somme de k=1 à n+1 de k.2^(k-1) vaut n.2^(n+1) + 1,
ainsi que quel que soit n de N, à partir de n >= 3, n! >= 2.3^(n-2).
Voilà, alors j'imagine que pour ces deux démo il faut utiliser un raisonnement par récurrence, or je bloque :/
Pour la première démo, je décompose la somme jusqu'à n+2, pour appliquer ce qu'on suppose au début de la récurrence, mais je n'arrive pas à retomber sur ce qu'il faut à la fin :(
Pour la seconde démo, je dis que (n+1)! = (n+1)*n!, puis je repars de ce que j'ai supposé : n! >= 2.3^(n-2), en multipliant par (n+1), mais idem, je n'aboutis pas au résultat recherché.. Merci d'avance ;D
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 03 Nov 2010, 17:30
par girdav » 03 Nov 2010, 17:30
Pour la seconde on écrit que
!\geq 3n!)
pour
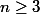
.
-
Mobster
- Membre Relatif
- Messages: 241
- Enregistré le: 29 Oct 2008, 20:42
-
 par Mobster » 04 Nov 2010, 15:44
par Mobster » 04 Nov 2010, 15:44
Comment montres-tu ça ? Je cherche mais ne trouve pas :/
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Nov 2010, 16:45
par arnaud32 » 04 Nov 2010, 16:45
n+1>3
tu multiples par n! ...
-
Mobster
- Membre Relatif
- Messages: 241
- Enregistré le: 29 Oct 2008, 20:42
-
 par Mobster » 04 Nov 2010, 16:54
par Mobster » 04 Nov 2010, 16:54
Ah oui, en effet.
Mais je vois pas comment retomber sur >= ce qu'il faut démontrer :X
-
Mobster
- Membre Relatif
- Messages: 241
- Enregistré le: 29 Oct 2008, 20:42
-
 par Mobster » 04 Nov 2010, 16:56
par Mobster » 04 Nov 2010, 16:56
Ha bah non, c'est bon, halleluja \o/
Merci bien mes frayres !
-
Mobster
- Membre Relatif
- Messages: 241
- Enregistré le: 29 Oct 2008, 20:42
-
 par Mobster » 04 Nov 2010, 16:57
par Mobster » 04 Nov 2010, 16:57
C'est fait pour la deuxième alors :) par contre personne n'a de piste pour la première ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Nov 2010, 17:08
par arnaud32 » 04 Nov 2010, 17:08
Mobster a écrit:C'est fait pour la deuxième alors

par contre personne n'a de piste pour la première ?
tu ecris ta somme a l'ordre n+1 donc jusqu'a n+2, tu sors le dernier terme (celui en n+2)
tu appliques ton hyp de recurence
tu vas tomber sur
2^{n+1} = (2n+2)2^{n+1}+1=2(n+1)2^{n+1}+1=(n+1)2^{n+2}+1)
-
Mobster
- Membre Relatif
- Messages: 241
- Enregistré le: 29 Oct 2008, 20:42
-
 par Mobster » 04 Nov 2010, 17:24
par Mobster » 04 Nov 2010, 17:24
J'ai compris pourquoi j'trouvais pas, au lieu d'avoir 2^(n+1) j'avais laissé k^(n+1) -__-! J'risquais pas de trouver ^^'
Merci beaucoup :) !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
