Probléme nombre complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
snemder7ay7a
- Membre Naturel
- Messages: 16
- Enregistré le: 03 Nov 2010, 12:52
-
 par snemder7ay7a » 03 Nov 2010, 13:08
par snemder7ay7a » 03 Nov 2010, 13:08
je ne sais quoi faire pour résoudre ce problème
montrer à l'aide des nombres complexes que
cos(pi/11)+ cos(3pi/11)+cos(5pi/11)+cos(7pi/11)+cos(9pi/11)=1/2
merci d'avance

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 03 Nov 2010, 13:11
par Ericovitchi » 03 Nov 2010, 13:11
les cos (kpi/11) sont les parties réelles de

donc il te reste à additionner les termes d'une suite géométrique
-
snemder7ay7a
- Membre Naturel
- Messages: 16
- Enregistré le: 03 Nov 2010, 12:52
-
 par snemder7ay7a » 03 Nov 2010, 15:15
par snemder7ay7a » 03 Nov 2010, 15:15
le problem c qu on n'a pas encore étudié la notation experimentale donc il me fait trouver une autre methode

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 03 Nov 2010, 15:33
par Ericovitchi » 03 Nov 2010, 15:33
Alors tu appelles C= cos(pi/11)+ cos(3pi/11)+cos(5pi/11)+cos(7pi/11)+cos(9pi/11)
et S= sin(pi/11)+ sin(3pi/11)+sin(5pi/11)+sin(7pi/11)+sin(9pi/11)
intéresse toi à C+iS
-
snemder7ay7a
- Membre Naturel
- Messages: 16
- Enregistré le: 03 Nov 2010, 12:52
-
 par snemder7ay7a » 03 Nov 2010, 16:27
par snemder7ay7a » 03 Nov 2010, 16:27
c ne donne rien parce la somme des arguments n'est pas egale a pi/3 dont le cos est 1/2

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 03 Nov 2010, 16:40
par Ericovitchi » 03 Nov 2010, 16:40
de toute façon l'argument d'une somme n'est pas la somme des arguments donc ça t'aura évité d'écrire des choses fausses.
Par contre si tu écris q=cos(pi/11) + i sin (pi/11) par exemple alors q^3= cos(3pi/11) + i sin (3pi/11) , etc... (en fait c'est l'argument d'un produit qui vaut la somme des arguments)
Donc C+iS peut s'écrire q+q^3+q^5+q^7+q^9, et donc .... ?
-
snemder7ay7a
- Membre Naturel
- Messages: 16
- Enregistré le: 03 Nov 2010, 12:52
-
 par snemder7ay7a » 03 Nov 2010, 17:13
par snemder7ay7a » 03 Nov 2010, 17:13
d'apreés la question j'ai compris qu'il faut démontrer que les sinkpi/11 sont egaux au sin pi/3. donc il faut reecrire la somme en un produit. supposons que j'ai facteurisé avec q cela ne va pas me donner le resultat puisque je cherche pi/3

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 03 Nov 2010, 18:36
par Ericovitchi » 03 Nov 2010, 18:36
q+q^3+q^5+q^7+q^9 c'est la somme des termes d'une suite géométrique
rappelons que
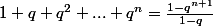
-
snemder7ay7a
- Membre Naturel
- Messages: 16
- Enregistré le: 03 Nov 2010, 12:52
-
 par snemder7ay7a » 03 Nov 2010, 21:36
par snemder7ay7a » 03 Nov 2010, 21:36
merci infiniment faut dire que jai oublié mes cours sur les suites
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 106 invités
