Dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
roro34720
- Membre Naturel
- Messages: 33
- Enregistré le: 17 Oct 2008, 17:44
-
 par roro34720 » 01 Nov 2010, 12:39
par roro34720 » 01 Nov 2010, 12:39
Soit la fonction f définie par
f(o)=0
f(x)=-x²+x²lnx si x appartient R+
étudier la continuité de d et sa dérivabilité en 0 ?
Etudier la fonction ?
je ne sais pas comme faire et par ou commencer merci de votre aide precieuse !!
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Nov 2010, 12:41
par girdav » 01 Nov 2010, 12:41
Bonjour,
il faut rajouter une étoile à

dans la définition.
Je pense que tu vois qu'il y a continuité sur
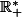
; il reste donc à montrer la continuité en

pour achever la première partie de la première question.
-
roro34720
- Membre Naturel
- Messages: 33
- Enregistré le: 17 Oct 2008, 17:44
-
 par roro34720 » 01 Nov 2010, 13:02
par roro34720 » 01 Nov 2010, 13:02
La continuit�e d'une fonction r�eelle peut se traduire par le fait que sa
courbe repr�esentative peut ^etre trac�ee d'un seul tenant, sans lever le crayon mais comment le prouver ?
-
Bill BM
- Membre Naturel
- Messages: 69
- Enregistré le: 18 Juin 2008, 21:49
-
 par Bill BM » 01 Nov 2010, 13:10
par Bill BM » 01 Nov 2010, 13:10
J'ai souvent vu utililiser le fait que l'ensemble de dérivabilité est l'ensemble de définition de la dérivée pour montrer qu'une fonction est dérivable en un point. Si c'est le cas...
-
roro34720
- Membre Naturel
- Messages: 33
- Enregistré le: 17 Oct 2008, 17:44
-
 par roro34720 » 01 Nov 2010, 13:15
par roro34720 » 01 Nov 2010, 13:15
pouvez vous me montrer pour cet exercice ? parce que je ne sais vraiment pas comment faire ! :mur:
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 01 Nov 2010, 13:21
par Matt_01 » 01 Nov 2010, 13:21
f est continue en

ssi
)
tend vers
)
quand

tend vers

.
Ici
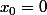
.
-
Bill BM
- Membre Naturel
- Messages: 69
- Enregistré le: 18 Juin 2008, 21:49
-
 par Bill BM » 01 Nov 2010, 13:23
par Bill BM » 01 Nov 2010, 13:23
T'as la fonction x² , la fonction x et la fonction xlnx, les 3 ont pour limites 0 en 0, tu obtiens la continuité. Pour la dérivabilité, parait qu'une fonction est dérivable partout où sa dérivée est définie...
Mais pourquoi tu viens ici avec ce problème? C'est pour lycée.
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 01 Nov 2010, 18:02
par jack01 » 01 Nov 2010, 18:02
n'oblier pas que
=0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
