La densité

[crazymaths]

bonsoir à tous!
s'il vous plait comment on peut démontrer cela :soit Aune partie non vide de R vérifiant les deux propriétés suivantes: si a,b dans A ; alors (a+b)\2 dans A
quel que soit x dans A,il existe a,b dans A, tel que x entre a et b.
Montrer que A est par tout dense dans R

tout d'abord, je vois pas trés bien comment démontrer généralement qu'une partie est dense dans un ensemble
et evidemment j'ai pas arrivé à resourdre cet exercice.
s'il vous plait, veuillez etre un peu clair dans votre reponse.
et merci beaucoup d'avance pour votre précieux aide.

[dibeteriou]

Bon alors pour prouver que A est dense dans R, on va prendre 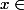R et montrer que pour tout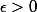 est approché par un élément de A à près.

Soit donc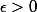 fixé. Il existe deux éléments a et b de A tels que a<x<b.
Désormais la deuxième propriété ne va plus servir (attention à la faute dans ton énoncé !).

On a deux approximations de x : une par excès et une par défaut. Maintenant, on a aussi dans A ; c est une "meilleure" approximation de x, et on peut remplacer a ou b par c de sorte qu'on ait toujours une approximation par excès et une par défaut.

Le principe est de recommencer ad vitam eternam. Calcule l'écart entre les deux approximations, il tend vers 0. Cherche à comprendre pourquoi ceci assure que x est approché à epsilon près.
Un dessin est chaudement recommandé :lol3: