Baryecntre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 17:10
par lea2007 » 31 Oct 2010, 17:10
salut à tous
voila c'est vacance, jai un devoir maison de maths sur les barycentres, mais je n'y comprend rien à cette notion .
voici l'énoncé de la premiere question que je n'arrive pas à faire :
ABC est un triangle, I,J et G sont les points définis par
AI = -2AB , AJ = 4/7AC et CG = 1/5CI
Exprimer I comme un barycentre de A et B puis G comme barycentre de C et I .
il me semble avoir trouvé quelque chose, pouvez vs me dire si c'est bien cela ?
IB= 2IA I BARYCENTRE DE (B,1)(A, -2)
IG= 4GC -GI - 4GC = 0 G barycentre de ( I, -1)(C, -4)
merci
lea2007 est connecté maintenant Bookmark and Share
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 17:18
par Arnaud-29-31 » 31 Oct 2010, 17:18
Salut,
Si tu veux exprimer I comme barycentre de A et B, il faut que tu trouve deux réels a et b tels que
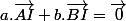
... Tu as déjà
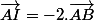
, il te manque plus qu'a exprimer
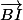
grâce à une relation de Chasles.
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 17:21
par lea2007 » 31 Oct 2010, 17:21
Arnaud-29-31 a écrit:Salut,
Si tu veux exprimer I comme barycentre de A et B, il faut que tu trouve deux réels a et b tels que
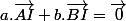
... Tu as déjà
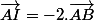
, il te manque plus qu'a exprimer
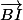
grâce à une relation de Chasles.
merci
ce qui veut dire que ce que j'ai fait est faux ...
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 17:38
par Arnaud-29-31 » 31 Oct 2010, 17:38
La méthode à l'air bonne mais tu n'as pas le bon résultat.
Comment as tu trouvé
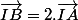
?
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 17:39
par lea2007 » 31 Oct 2010, 17:39
Arnaud-29-31 a écrit:La méthode à l'air bonne mais tu n'as pas le bon résultat.
Comment as tu trouvé
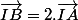
?
j'ai tout simplement fais un schéma, j'ai représenté les vecteurs ...
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 17:40
par Arnaud-29-31 » 31 Oct 2010, 17:40
Il faut décomposer les vecteurs en utilisant la relation de Chasles.
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 17:48
par lea2007 » 31 Oct 2010, 17:48
est ce correct ?
AI= -2 AB
AI = -2AI -2 IB
dc I barycentre de (A, -2) ( B, -2)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 17:49
par Arnaud-29-31 » 31 Oct 2010, 17:49
Oulaaa ... non il faut regrouper les AI avant de conclure.
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 17:53
par lea2007 » 31 Oct 2010, 17:53
ah oui c vrai , dsl
AI = -2AI -2 IB
3AI = -2IB
3AI +2IB = 0
-3IA + 2IB = 0
DC I BAR DE ( A, -3) ( B,2)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 17:55
par Arnaud-29-31 » 31 Oct 2010, 17:55
Oui, c'est mieux :)
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 17:57
par lea2007 » 31 Oct 2010, 17:57
je te remercie pr tn aide précieuse .
a bientot
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 18:03
par Arnaud-29-31 » 31 Oct 2010, 18:03
De rien :)
Bonne soirée, à bientôt !
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 18:16
par lea2007 » 31 Oct 2010, 18:16
dsl de te déranger encore !
CG = 1/5 CI
CG = 1/5 CG + 1/5 GI
CG -1/5 CG = 0
4/5 CG - 1/5 GI = 0
-4/5 GC -1/5 GI = 0
g barycentre de ( C, -4/5) ( I, -1/5)
c juste , merci bcp ...
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 18:19
par Arnaud-29-31 » 31 Oct 2010, 18:19
Oui c'est juste mai son aurait pu multiplier la dernière expression par -5 ... et ainsi obtenir
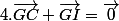
-
lea2007
- Membre Naturel
- Messages: 10
- Enregistré le: 31 Oct 2010, 17:06
-
 par lea2007 » 31 Oct 2010, 18:31
par lea2007 » 31 Oct 2010, 18:31
pr prouver que g est barycentre de ( A,3) ( b, -2) et (c , 4)
je dois multiplier par -1 le barycentre de I ( dc A et B ) mais comment ce fait il que je prend que pr le barycentre de G , je dois simplement prendre le point (C, 4)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 31 Oct 2010, 18:46
par Arnaud-29-31 » 31 Oct 2010, 18:46
Tu peux réutiliser les relations vectoriels et trouver a,b,c tels que a.AG + b.BG + c.CG = 0 ou alors utiliser les lois de barycentre partiels.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
