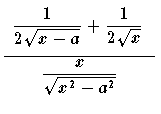Limite en a de forme indeterminée

[dam63]

Bonjour,

J'ai un exercice dans le cadre d'un soutien mathématique pour les étudiants venant de DUT.
Mon niveau BAC S + "équivalence en 0"

Soit a>0.
Donnez la limite en a de la fonction définie par :
racine(x) - racine(a) + racine(x-a)
------------------------
racine(x2 - a2)

J'ai essayé toute sorte de factorisation ... pour toujours finir dans un mur ou au point de départ !
Pouvez vous m'aider à démarrer ?
Par exemple avec la règle de L'Hospital mais je bloque ici après avoir dérivé numérateur et dénominateur :


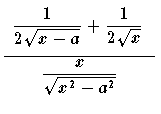
En suivant se tuto :
http://limite.cours-de-math.eu/regle-hopital.php
Quand je remplace x par a le premier terme est une division par 0
Donc je suis bloqué là.

Par avance merci.
Bonne soirée !

[fourize]

salut :)

mais pourquoi t'eleve pas le numerateur et le denominateur au carré,
et puis de dire que la limite d'un polynome est egale à la limite du
monome de plus haut degré après simplification !!! ???

ça devait marcher ...

[Ben314]

Salut,
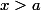
Pour tout , on a donc

[dam63]

@fourize : mais si j'élève au carré je me retrouve avec a²-b² en dénominateur donc quand x tend vers a on à toujours 0 au dénominateur et en haut certaine racine ne se simplifie pas on se retrouve avec des racines de a^3, x^3 ...

@Ben314 : Je comprend se que tu as fait mais je ne voit pas ou tu veut en venir ? Je n'est aucune idée de comment développer votre formule pour avoir une limite en a !

Merci à vous deux pour les réponses et j'espère que vous pourrez à nouveau me débloquer.

[Ben314]

@Ben314 : Je comprend se que tu as fait mais je ne voit pas ou tu veut en venir ? Je n'est aucune idée de comment développer votre formule pour avoir une limite en a !

Il ne faut SURTOUT PAS développer !!!!!
Dans une indetermination 0/0, le but est de FACTORISER le numérateur et le dénominateur de façon à pouvoir simplifier en haut et en bas par des trucs qui tendent vers 0.
Ici, je t'ai donné les "bonnes" factorisations, il ne te reste plus qu'à faire les simplifications !!!

Pour la deuxième fraction, la simplification est triviale, pour la première, elle l'est un tout petit peu moins ( A/racine(A)=... )

[dam63]

Merci beaucoup je crois avoir réussi !
Voila ma copie ! Désolé pour les yeux...



Encore merci et bonne journée à tous. :lol3:

[Ben314]

C'est impeccable.

Bon, sinon, il y a surement d'autres méthodes (en particulier en utilisant astucieusement la "règle de l'hospital) mais celle là est assez simple et naturelle (on cherche le plus possible à factoriser un truc qui tend vers 0 lorsque x tend vers a)

[dibeteriou]

Attention à ne pas confondre égalité (entre expressions algébriques) et équivalence (entre phrases logiques) !

[Hir]

1ere fois que j'entends parler de cette règle de L'Hospital !
C'est assez étrange qu'elle ne soit pas dans les programmes de lycées, ça parait être assez efficace comme règle, non ?
Au niveau prépa par contre c'est sur qu'avec les DL, on peut largement s'en passer

[Ben314]

1ere fois que j'entends parler de cette règle de L'Hospital !
C'est assez étrange qu'elle ne soit pas dans les programmes de lycées, ça parait être assez efficace comme règle, non ?
Au niveau prépa par contre c'est sur qu'avec les DL, on peut largement s'en passer

Si ça peut te rassurer, ben à mon époque, je suis pas sûr d'en avoir entendu parler non plus : Au Lycée, ben on faisait des (gros) calculs pour les limites, ce qui est pas totalement con, en particulier pour... apprendre à calculer !!!
Puis, à la fac, ben les D.L. c'était le début de l'analyse de première année donc on faisait de nouveau des calculs, mais... plus les mêmes !!!