mathilde.guelen a écrit:C'est complique .... :triste:
pas temps que ça (et puis c'est pas triste...)
mathilde.guelen a écrit:Mais tu ne va que jusque
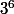
, pourquoi pas
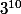
en fait ?
Pour au moins 2 raisons :
1) Dés que l'on trouve un entier

tel que

(modulo 7), c'est totalement inutile d'aller "plus loin" vu que cela implique que

,

,

... c'est à dire que les puissance suivantes sont les mêmes que les premières puissances calculées.
Par exemple, sans calculs suplémentaires, ben je sais que
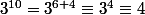
2) Si je commence par écrire que

(modulo 7), et que je veut en déduire des choses concernant

, ben ça sent le début d'une récurrence (avec n=1) et ça semble assez malin, mais, rien que pour passer au rang n=2, il faut évaluer modulo 7 la quantité
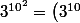^{10}\equiv 4^{10})
(modulo 7) et il faudrait refaire les calculs des

modulo 7 pour aller plus loin.
Alors que, pour ce cas n=2, il est nettement plus rapide d'écrire
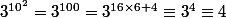
(modulo 7)
Edit : En fait, l'idée de commencer par évaluer

(modulo 7) puis
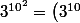^{10}\equiv 4^{10})
(modulo 7) marche relativement bien aussi car on a

(modulo 7) donc
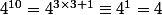
...
, pourquoi pas
en fait ?