Arithmétique dans Z[sqrt(-5)]

[Doraki]

Soit
A est muni d'une addition et d'une multiplication.

Pour tout dans A, on note , le conjugué de :
si alors ,
et on note

N est un morphisme de monoïdes de dans

Montrer par récurrence que tout nombre premier p (dans ), on est dans l'une des trois situations suivantes :

a) -5 n'est pas un carré modulo p, et
pour tout x de A, N(x) est multiple de p (dans ) x est multiple de p (dans A).

b) -5 est un carré modulo p, il existe u dans A tel que N(u) = p, et
pour tout x de A, N(x) est multiple de p (dans ) x est multiple de u ou de (dans A).

c) -5 est un carré modulo p, il existe u dans A tel que N(u) = 2p,et
pour tout x de A, N(x) est multiple de 2p (dans ) x est multiple de u ou de (dans A).

[benekire2]

Salut ,

Je le regarderais :zen:
Ca fait un peu echo au problème aque j'avais posé qui partait en délire dans .. c'est cool :happy2:

[Doraki]

Ouais sauf qu'ici c'est un peu moins simple, y'a pas de pgcd ou de décomposition unique en facteurs premiers.
L'exercice donne justement un moyen de voir l'obstruction à ça (sans parler d'idéaux).

Le tout reste élémentaire tant que tu sais faire de l'arithmétique dans Z/pZ et dans Z.

[ffpower]

'lut
a)Y'a un sens trivial : si x=py, alors N(x)=p²N(y) donc N(x) multiple de p ( et même de p² )
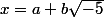
et un autre sens pas bien dur : Si et si p divise N(x)=a²+5b², alors si b n'était pas divisible par p il serait inversible modulo p et on aurait (a/b)^2=-5 mod p, ce qui contredit l' hypothèse. b est donc divisible par p, par suite, a aussi et x est un multiple de p dans A.

b) ( pas mal galéré pour celui là )
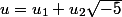
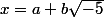
On suppose qu'il existe tel que , et soit alors tel que p divise N(x). Alors on a modulo p :

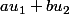
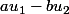
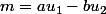
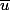
donc soit , soit est divisible par p, disons que c'est ( quitte à remplacer par ). En particulier, m est un multiple de u dans A. En constatant les identités


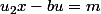
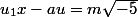
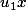
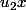
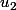
on en déduit que et sont des multiples de u dans A, et en faisant un Bezout ( dans N ) entre et ( dont on vérifie facilement qu'ils sont premiers entre eux ), on en déduit que x est un multiple de u

c) J'ai pas vérifié, mais je suppose que ça se passe pareil que pour b)

Aprés reste à montrer que ce sont les 3 seules configurations possibles, autrement dit que si -5 est un carré, alors il existe u tel que N(u)=p ou 2p. Pour ce faire j'ai essayé le même argument que pour déterminer les premiers somme de 2 carrés ( principe des tiroirs ), mais au final j'obtiens seulement l'existence de u tel que N(u)=p,2p ou 3p. Me reste donc encore à bosser un petit peu pour virer ce cas en trop^^

[Doraki]

Tu as inversé a et b, mais chuis d'accord que ça implique au2+-bu1 = 0 mod p
Le reste m'a l'air de marcher même si c'est un peu laborieux.

Etablir l'équivalence dans le cas c) devrait pas être beaucoup plus dur mais y'a quand même des trucs à dire.


Bon après il faut en effet prouver que si -5 est un carré modulo p, on trouve un u de norme p ou 2p.
C'est là que le "montrer par récurrence" il aide.

Je savais pas qu'il y avait un argument utilisant le principe des tiroirs pour déterminer les premiers somme de deux carrés.

[qshanshan]

Je savais pas qu'il y avait un argument utilisant TN Requin|Tn Requin|Air Max 90|Tn|Tn Requinle principe des tiroirs pour déterminer les premiers somme de deux carrés.

[ffpower]

Tu as inversé a et b, mais chuis d'accord que ça implique au2+-bu1 = 0 mod p

Exact, j'éditerais quand (si?) j'en aurai à nouveau l'occasion ( au passage tout le monde peut voir que rien ne nuit à la compréhension du topic suite à une édition pour corriger la coquille, pour peu que le passage erroné soit cité. je ferme la parenthese )

Le reste m'a l'air de marcher même si c'est un peu laborieux.

Si seulement tu avais vu ma démo initiale, tu aurais vu le véritable sens de laborieux XD. T'as une version courte?

Je savais pas qu'il y avait un argument utilisant le principe des tiroirs pour déterminer les premiers somme de deux carrés.

L'argument est le suivant : soit s une racine de -1 mod p. Grace au principe des tiroirs, on peut trouver a,b non nuls compris entre -racine(p) et racine(p) tels que a+sb=0 mod p, et donc a²+b²=0 mod p. Ainsi a²+b² est un multiple de p strictement plus petit que 2p, donc c'est p.

En adaptant l'argument ici, on obtient un u tel que N(u) multiple de p et N(u)u divisible par 2.

Bon avec ma réduction précédente, j'aurais pu me contenter d'étudier le cas k=3, mais pour ce que ça change..

[Doraki]

J'avais sauté le mot réccurence, effectivement ça aide. Du coup : il existe u tel que N(u) soit divisible par p, et N(u)u divisible par 2.

Ce que tu dois vérifier en montrant que 2 est dans le cas c)
(s'il n'y était pas, bah on serait comme dans Z[i] ou Z[sqrt(-2)], et y'aurait jamais de cas c))

Pour une preuve moins laborieuse de la divisibilité dans le cas b) :
En reprenant tes notations, on voit aisément que a/b = u1/u2 mod p, (ou la même avec -u2)
Dans ce cas, on pose .
En regardant les composantes modulo p, il existe k tel que x = ku, donc . Donc on peut bien diviser par p.

[ffpower]

Ok, effectivement, c'est plus court ( et moins "bidouillesque" ). Exo sympa, ça faisait un ptit moment que j'avais pas fait d'arithmétique^^

[Ben314]

Salut,
Concernant les "3 cas", ne peut on pas s'en sortir avec le "théorème des tiroirs", mais en prenant entre et entre (où ) ?

[Doraki]

Si j'ai bien fait mes calculs, ça permet de remplacer le facteur 6 de ffpower par un facteur .
Et si on utilise le principe des tiroirs simplement dans une boule (N(x) <=),
on obtient un facteur , (la borne de Minkowski), qui est < 3.

Dans Z[sqrt(-6)], cette borne dépasse 3, mais l'exo s'adapte bien et marche toujours.

Question subsidiaire :
Montrer que la classe de p mod 20 détermine dans lequel des cas on se trouve.

[ffpower]

J'avais pensé au coup des rectangles mais j'ai vite déchanté. J'ai pas pensé à prendre directement la bonne boule, effectivement ca a l air mieux ainsi^^

PS : l'exo ne s'adapterait il pas à tous les , quitte à avoir plus de 3 cas? Y a t il des valeurs qui font completement buguer la démo?

[Doraki]

Bah ça m'a l'air de bien marcher.

Pour -7, l'anneau des entiers qui correspond c'est (il est principal) et pas

Si on fait pas gaffe et qu'on ne rajoute pas cet élément, ça fait un peu bizarre pour p=2 :
Dans A = , si , aucune puissance de u (à part u^0) n'est dans A,
ce qui fait qu'on a une infinité d'éléments irréductibles de A, de normes 4,8,16,32,...
etc.

Pas tellement simple à expliquer quand on reste dans alors que tout va bien dans

[Ben314]

Bon, ça fait un moment que je glandouille à... rien trouver...
Le fait que -5 soit un carré modulo p ssi p congru à ?,?,?... modulo 20, jusque là, ça va (réciprocité quadatique) mais, par contre je ne vois pas par quel bout m'y prendre ne serait-ce que pour montrer que les cas b) et c) sont exclusifs...

[ffpower]

Supposons p=a²+5b², 2q=c²+5d² avec p=q mod 20. En regardant le tout mod 5, ça donne c²=2a² mod 5. Et vu que 2 n'est pas un carré, a=c=0 mod 5, et donc p et q sont divisible par 5, donc p=q=5..

[Doraki]

Ca me va.

On peut aussi simplement dire que pour p impair,
en regardant mod 4, p = a²+5b² => p = 1 mod 4
en regardant mod 8, 2p = a²+5b² => p = 3 mod 4

[Ben314]

Effectivement...
Je cherchais nettement plus complexe en partant de a²+5=kp et en essayant de "compter" les facteurs de k dans le cas b) et ceux dans le cas c)...