Lieu géométrique de barycentres-1erS

[christophe018]

Bonjour ,j'ai un devoir maison à rendre pour la rentrée sur le lieu géométrique de barycentres.
J'ai répondu à toutes les questions du devoir. la dernière question me laisse perplexe .Je n'ai pas très bien compris ce point de la leçon.Pouvez vous m'aider à corriger ou à confirmer ma réponse ?
Merci bien .

Ennoncé : Soit A, B,C trois points distincts du plan,k un nombre réel.
On appelle Gk le barycentre de la famille des points pondérés (A ;2k+1) (B ;6k-1) (C ;k-1).


3.Déterminer et construire le lieu géométrique des points GK quand K varie dans R\ {1/9}.(A partir de l'égalité vectorielle définnisant Gk ,on fera intervenir le barycentre H des points (A ;2) (B ;6) (C ;1) et le barycentre G0.)

Ma réponse :
1.Déterminons le lieu géométrique des points Gk tels que :
.H barycentre des points pondérés (A ;2) (B ;6) (C ;1)
.G0 barycentre des points pondérés ( A ;1) B ;-1) C ;-1)

2.Soit H barycentre de (A ;2) (B ;6) (C ;1),on a alors pour tout point H du plan :
2HA+6HB+1HC=9HG

Soit G barycentre de (A ; 1) (B ;-1) (C ;-1) on a alors pour tout point G du plan :
1GA-1GB-1GC=-1GG

3.On trouve 9HG=-1GG
Donc HG=1/9 GG .

Le lieu géométrique des points Gk est donc le cercle G1 et 1/9 GG=1

[Jimm15]

Bonjour,

Les relations que tu as écrites sont fausses.


Voici les correctes :


Puisque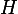 est barycentre des points pondérés , et (), alors on peut écrire :




Puisque est barycentre des points pondérés , et (), alors on peut écrire :




Puisque est barycentre des points pondérés , et ( puisque ), alors on peut écrire :





L’énoncé précise bien :

A partir de l'égalité vectorielle définnisant Gk ,on fera intervenir le barycentre H des points (A ;2) (B ;6) (C ;1) et le barycentre G0

À toi de voir comment tu peux faire.

[christophe018]

Bonjour,

Les relations que tu as écrites sont fausses.


Voici les correctes :


Puisque est barycentre des points pondérés , et (), alors on peut écrire :




Puisque est barycentre des points pondérés , et (), alors on peut écrire :




Puisque est barycentre des points pondérés , et ( puisque ), alors on peut écrire :





L’énoncé précise bien :À toi de voir comment tu peux faire.

d'accord ,vous venez de traduire l'énoncée en barycentre.Mais je n'arrive toujours pas à voir comment construire ce lieu géométrique.Je vous montre ci joint ce que j'ai essayé.

Voici mes résultats.( je n'indique pas dans le topic le dévellopement pour gagner de la place).

.G0 barycentre des points pondérés (A;1) (B;-1) (C;-1)
donc
AG0=1AB+1AC

.H barycentre des points pondérés (A;6) (B;2) (C;1)
donc
HA=1/9 (6AB+1AC)

.GK barycentre des points pondérés (A;2k+1) (B;6k-1) (C;k-1)
donc
AGk= 1/9k-1 (6AB+1AC)

Que dois je faire maintenant.
Puis je réduire en indiquant que AGk= 1/9 (1AB+1AC)?
Etant donné que 6AB+1AC-6AB-1AC=0

[Jimm15]

Coucou,

Si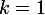 , remarques-tu alors que les coefficients de la relation vectorielle établie pour « correspondent » aux coefficients concernant les deux autres barycentres ?
Par exemple : . Cela ressemble étrangement à , non ?

L’idée va donc ici de partir de la relation vectorielle définissant puis de faire intervenir les deux autres barycentres judicieusement.
Tu peux commencer par développer comme je l’ai fait ci-dessus puis de faire intervenir les points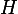 et .

[Jimm15]

d'accord ,vous venez de traduire l'énoncée en barycentre.Mais je n'arrive toujours pas à voir comment construire ce lieu géométrique.Je vous montre ci joint ce que j'ai essayé.

Voici mes résultats.( je n'indique pas dans le topic le dévellopement pour gagner de la place).

.G0 barycentre des points pondérés (A;1) (B;-1) (C;-1)
donc
AG0=1AB+1AC

.H barycentre des points pondérés (A;6) (B;2) (C;1)
donc
HA=1/9 (6AB+1AC) ==> Attention ! C’est . Sinon, il faut changer tous les signes...

.GK barycentre des points pondérés (A;2k+1) (B;6k-1) (C;k-1)
donc
AGk= 1/9k-1 (6AB+1AC) ==> Où sont passés les ??
C’est plutôt .

Que dois je faire maintenant.
Puis je réduire en indiquant que AGk= 1/9 (1AB+1AC)? ==> Aucun sens !!
Etant donné que 6AB+1AC-6AB-1AC=0

Tu vas un peu trop vite.

[christophe018]

Tu vas un peu trop vite.

Oui ,merci je vois que je suis allé un peu trop vite en rédigeant sur l'ordinateur.Mais que puis-je faire?
Puis je supprimer les K maintenant ?

[Jimm15]

Non. Fais plutôt comme je te l’ai conseillé dans mon message de 18h38.

[christophe018]

Non. Fais plutôt comme je te l’ai conseillé dans mon message de 18h38.

d'accord ,alors voici ma réponse

(2+1)GkA+(6-1)GkB+(1-1)GkC=0
2GkA+1GkA+6GkB-1GkB+1GkC-1GkC=0
3GkA+5GkB=0
3GkA+5GkB+5AB=0
5AB=8AGk
AGk=5/8AB

[Jimm15]

d'accord ,alors voici ma réponse

(2+1)GkA+(6-1)GkB+(1-1)GkC=0
2GkA+1GkA+6GkB-1GkB+1GkC-1GkC=0
3GkA+5GkB=0
3GkA+5GkB+5AB=0
5AB=8AGk
AGk=5/8AB

Je ne t’ai pas dit de remplacer par ! On ne sait rien de sa valeur !! C’était juste pour te montrer comment procéder afin de faire intervenir les deux autres barycentres judicieusement, ce que tu n’as d’ailleurs pas fait...

Recommence en laissant les et en faisant intervenir et judicieusement.

[christophe018]

Je ne t’ai pas dit de remplacer par ! On ne sait rien de sa valeur !! C’était juste pour te montrer comment procéder afin de faire intervenir les deux autres barycentres judicieusement, ce que tu n’as d’ailleurs pas fait...

Recommence en laissant les et en faisant intervenir et judicieusement.

C'est ce que j'ai également fais sur mon brouillon.Mais,je ne comprends pas la suite du résonnement .Il restera toujours le barycentre H et G0.Montrez moi ,comment résoudre ce problème s'il vous plait ?

[Jimm15]

Salut,



À toi de terminer.

[christophe018]

Salut,



À toi de terminer.

d'accord merci pour votre réponse .Donc il me reste à faire cette démarche.La voici

9kGkH-GKGo=0
9kGkH-1KGKH-1kHG0=0
-1kHG0=8kHGk
HGk=-1/8HGo

c'est bien?
Mais je ne vois pas comment maintenant je pourrais construire le lieu géométrique.

[Jimm15]

d'accord merci pour votre réponse .Donc il me reste à faire cette démarche.La voici

9kGkH-GKGo=0
9kGkH-1KGKH-1kHG0=0
-1kHG0=8kHGk
HGk=-1/8HGo

c'est bien?
Mais je ne vois pas comment maintenant je pourrais construire le lieu géométrique.

Puisque varie, il n’y a pas ici à chercher où placer précisément, puisqu’il va varier !

Quand on a , on peut donc écrire .
Comment qualifie-t-on alors les deux vecteurs ? Qu’en déduit-on pour les trois points , et ?

[christophe018]

Puisque varie, il n’y a pas ici à chercher où placer précisément, puisqu’il va varier !

Quand on a , on peut donc écrire .
Comment qualifie-t-on alors les deux vecteurs ? Qu’en déduit-on pour les trois points , et ?

les deux vecteurs sont ainsi colinéaires puisque deux vecteurs u et v sont colinéaires lorsqu'il existe un réel k tels que u=kv ou v=k*u
Les trois points ont donc le même sens,la même norme et la même direction.
donc les les points Gk, G0 et H sont alignés

[christophe018]

les deux vecteurs sont ainsi colinéaires puisque deux vecteurs u et v sont colinéaires lorsqu'il existe un réel k tels que u=kv ou v=k*u
Les trois points ont donc le même sens,la même norme et la même direction.
donc les les points Gk, G0 et H sont alignés

Merci pour toute votre aide .J'aurais juste une dernière question.Comment fait-on pour construire le lieu géométrique des points Gk?