saloute tout le monde
ozourdui...petites questions de mathématique qui me tracaces :)
1/ j'ai trop du mal a calculer 3 fonction dérivés ...
f(t)= -3 cos [2x - (pi/6) ] <= je ne sais pas quel formule appliqué (forme uv ou cos(ax +b) ? que devient le -3 ?! -_-')
f(t) = sint cos(3t) <= idem ! quel formule apliqué...a chaque fois je trouve un résultat différent -_-'
f(t) = tsin(2t) <= re-idem lol ! est ce que la dérivé de sin(2t) = cos(2t) ? quel est la dérivé de t ? 1 ? ...besoin d'aide je crois lol ^^'
f(x) = x - 1/x +[1/(x)^2] <= alors la, je nage! vraiment aucun idée, j'ai essayé plusieur méthodes : aucun résutat semblable ! comment calculer cette dérivé ? quel est finalement le résultat exact ?
2/ PAssons au barycentre ^^'
juste 2 pitites question, le reste j'ai su faire (ehehehe)
- on a AB=4cm et on cherche l'ensemble des points C tel que 3MA^2 +MB^2 =16 <= sans carré ca aurait été plus facile!
On me demande de justifier que A appartient a C ! ...j'avou ne pas avoir tout compris ^^'
On me demande de definir le barycentre G des pts pondérés etc..definir c'est quoi ? les coordonées ? sa position (AG = xAB ) ?
Merci d'avance a ceux qui prendront le temps lol
Dérivé + barycentre ^^'
3 messages
- Page 1 sur 1
Bonjour,
je vais te donner les réponses finales, et puis tu me diras comment on calcule les dérivées, OK?
Ici, je suppose que c'est=-3cos(2t - {\pi\over6})) .
.
=6sin(2t-{\pi\over6})) . On utilise la formule de la dérivée d'une fonction composée et le -3 devant est un coefficient.
. On utilise la formule de la dérivée d'une fonction composée et le -3 devant est un coefficient.
=cos(t)cos(3t)-3sin(3t)sin(t)) . On utilise la formule de la dérivée d'un produit et de la dérivée d'une fonction composée.
. On utilise la formule de la dérivée d'un produit et de la dérivée d'une fonction composée.
=sin(t)+2tcos(2t)) . C'est la même chose que la précédente.
. C'est la même chose que la précédente.
Enfin,=1+{1\over{x^2}}-{2\over{x^3}}) . On utilise la formule de la dérivée de
. On utilise la formule de la dérivée de 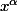 .
.
Bon courage,
Zeb.
je vais te donner les réponses finales, et puis tu me diras comment on calcule les dérivées, OK?
kronos a écrit:f(t)= -3 cos [2x - (pi/6) ] <= je ne sais pas quel formule appliqué (forme uv ou cos(ax +b) ? que devient le -3 ?! -_-')
Ici, je suppose que c'est
kronos a écrit:f(t) = sint cos(3t) <= idem ! quel formule apliqué...a chaque fois je trouve un résultat différent -_-'
kronos a écrit:f(t) = tsin(2t) <= re-idem lol ! est ce que la dérivé de sin(2t) = cos(2t) ? quel est la dérivé de t ? 1 ? ...besoin d'aide je crois lol ^^'
kronos a écrit:f(x) = x - 1/x +[1/(x)^2] <= alors la, je nage! vraiment aucun idée, j'ai essayé plusieur méthodes : aucun résutat semblable ! comment calculer cette dérivé ? quel est finalement le résultat exact ?
Enfin,
Bon courage,
Zeb.
Bonjour,
quelques indices pour les derivées ...
f(t)= -3 cos [2x - (pi/6) ]
f'(t)=-3*(2*(-sin(2x-(pi/6)))
car tu derives une fonction composée f(g(t)) avec f(x)= cos(x) et g(t)=2x-(pi/6) donc [f(g)]'(t)=f'(g(t))*g'(t) on remplace donc et ca nous donne :
[f(g)]'(t)=-sin(2x-(pi/6))*2 ca la derivée de la fonction cos est -sin ...
f(t) = sint cos(3t) t'applqieu la formule de la derivée de produit de deux fonctions a savoir
f(t)=g(t)*h(t) donc f'(t)= g'(t)*h(t)+g(t)*h'(t)
f'(t)=cos(t)*cos(3t)+sin(t)*(-3sin(3t))...
f(t) = tsin(2t) pour celle la idem ... mais tu fais une erreur la derivée de sin(2t)= 2 cos(2t) tu as une fonction composée ...
f(x) = x - 1/x +[1/(x)^2]
on va aller petit a petit :
la derivée de x est 1
la derivée de 1/x t'applique la formule pour une fraction si tu veux
(F/G)'=(F'G-G'F)/G²
la derivée de 1/x ca donne -1/x²
la derivée de 1/x² idem et tu dois trouver : -2x/x^4=-2/(x)^3
et donc en resultat finale puisque la derivé de somme de fonction est la somme des derivée
f'(t)=1-(-1/x²)+(-2/(x)^3)=1+1/(x)²-2/x^3...
quelques indices pour les derivées ...
f(t)= -3 cos [2x - (pi/6) ]
f'(t)=-3*(2*(-sin(2x-(pi/6)))
car tu derives une fonction composée f(g(t)) avec f(x)= cos(x) et g(t)=2x-(pi/6) donc [f(g)]'(t)=f'(g(t))*g'(t) on remplace donc et ca nous donne :
[f(g)]'(t)=-sin(2x-(pi/6))*2 ca la derivée de la fonction cos est -sin ...
f(t) = sint cos(3t) t'applqieu la formule de la derivée de produit de deux fonctions a savoir
f(t)=g(t)*h(t) donc f'(t)= g'(t)*h(t)+g(t)*h'(t)
f'(t)=cos(t)*cos(3t)+sin(t)*(-3sin(3t))...
f(t) = tsin(2t) pour celle la idem ... mais tu fais une erreur la derivée de sin(2t)= 2 cos(2t) tu as une fonction composée ...
f(x) = x - 1/x +[1/(x)^2]
on va aller petit a petit :
la derivée de x est 1
la derivée de 1/x t'applique la formule pour une fraction si tu veux
(F/G)'=(F'G-G'F)/G²
la derivée de 1/x ca donne -1/x²
la derivée de 1/x² idem et tu dois trouver : -2x/x^4=-2/(x)^3
et donc en resultat finale puisque la derivé de somme de fonction est la somme des derivée
f'(t)=1-(-1/x²)+(-2/(x)^3)=1+1/(x)²-2/x^3...
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 106 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
