Aide DM 1ere S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 15:15
par zepl0w » 26 Oct 2010, 15:15
Salut,
Si 1/x0 est solution de léquation (E) , on a 1/x0;) - 1/4x0³+1/2x0² -1/4x0 = 0
Mais c'est si simple que ça ?
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 16:16
par zepl0w » 26 Oct 2010, 16:16
J'ai oublié le +1.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Oct 2010, 16:23
par Sa Majesté » 26 Oct 2010, 16:23
zepl0w a écrit:Salut,
Si 1/x0 est solution de léquation (E) , on a 1/x0;) - 1/4x0³+1/2x0² -1/4x0 = 0
Mais c'est si simple que ça ?
Ça n'en avait pas l'air si j'en crois le début du post
Mais bon oui c'est ça (avec le +1)
EDIT : j'ai lu trop vite, non en fait tu t'es trompé
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 16:34
par zepl0w » 26 Oct 2010, 16:34
Si x0 est solution de léquation (E) , on a : x0;) - 4x0³ + 2x0² - 4x0 +1= 0 avec x0 différent de 0.
D'où 1/x0 différent de 0 donc 1/x0;) - 1/4x0³+1/2x0² -1/4x0 +1 = 0.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Oct 2010, 16:43
par Sa Majesté » 26 Oct 2010, 16:43
Reprenons calmement
Tu dois montrer que si x0 est une solution de (E) alors 1/x0 est aussi une solution de (E)
Ton hypothèse c'est "x0 est une solution de (E)" c'est-à-dire que tu supposes que x0;) - 4x0³ + 2x0² - 4x0 +1= 0
Tu dois montrer que 1/x0 est solution de (E), ce qui veut dire que tu dois montrer que ...
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 17:20
par zepl0w » 26 Oct 2010, 17:20
Je dois montrer que 1/x0;) - 1/4x0³+1/2x0² -1/4x0 +1 = 0 car x0 différent de 0 ?
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 18:20
par zepl0w » 26 Oct 2010, 18:20
Finalement je pense avoir trouvé.
Si x0 est solution de léquation (E) , on a : x0;) - 4x0³ + 2x0² - 4x0 +1= 0.
On divise des deux cotés par x0;) et on obtient 1 -4/x0 + 2/x0² -4/x0³+1/x0;) = 0 qui équivaut à (1/x0);) -4(1/x0)³ +2(1/x0)² -4(1/x0) +1 = 0
Donc 1/x0 est solution de l'équation (E).
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 18:37
par Jimm15 » 26 Oct 2010, 18:37
Oui, cest bon.
Il était aussi possible de remplacer
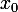
par

puis de multiplier par

et de voir quon retombait sur léquation de départ.
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 18:56
par zepl0w » 26 Oct 2010, 18:56
Ok merci.
Pour la question 3 il suffit d'écrire : (x0;) - 4x0³ + 2x0² - 4x0 +1)/ x²= 0 équivaut à x² - 4x + 2 - 4/x + 1/x² = 0 ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 19:12
par Jimm15 » 26 Oct 2010, 19:12
zepl0w a écrit:Ok merci.
Pour la question 3 il suffit d'écrire : (x0;) - 4x0³ + 2x0² - 4x0 +1)/ x²= 0 équivaut à x² - 4x + 2 - 4/x + 1/x² = 0 ?
Oui, pour tout

.
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 19:47
par zepl0w » 26 Oct 2010, 19:47
La réponse à la question 4: (x + 1/x)² est bien : x² + 3/x² ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 19:51
par Jimm15 » 26 Oct 2010, 19:51
zepl0w a écrit:La réponse à la question 4: (x + 1/x)² est bien : x² + 3/x² ?
Peux-tu détailler ton calcul ?
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 19:51
par zepl0w » 26 Oct 2010, 19:51
Je viens de me rendre compte de mon erreur.
La réponse est : x² + (2x² +1)/x² ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 19:55
par Jimm15 » 26 Oct 2010, 19:55
zepl0w a écrit:Je viens de me rendre compte de mon erreur.
Et tu trouves quoi finalement ?
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 20:05
par zepl0w » 26 Oct 2010, 20:05
J'ai édité.
Pour la question 5 je sais que je dois faire apparaître une équation de la forme ax² + bx + c = 0 mais je ne sais que avec X = x² ou X = ;)x.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 20:10
par Jimm15 » 26 Oct 2010, 20:10
Jobtiens ça également.
On peut aussi écrire

.
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 20:14
par zepl0w » 26 Oct 2010, 20:14
Oui je suis d'accord avec la 2eme forme et le 2nd terme est de la forme bx?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 20:21
par Jimm15 » 26 Oct 2010, 20:21
On a :
^2=x^2+\frac{1}{x^2}+2)
.
On pose

doù
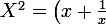^2=x^2+\frac{1}{x^2}+2)
.
À partir de là, que donne léquation suivante en fonction de
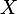
?

-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 20:21
par zepl0w » 26 Oct 2010, 20:21
On pose X = x + 1/x
D'où (E')= X² - 4X +2
C'est juste?
Vous avez été trop rapide. :lol3:
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 20:40
par zepl0w » 26 Oct 2010, 20:40
Ensuite je trouve X' = 2 - 2 racine de 2 et X'' = 2 + 2 racine de 2.
Mais ensuite pour trouver les solutions de (E) je bloque.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
