Mesure des aires planes

[goudou]

Bonjour à tous,

J'ai des petites difficultés à comprendre les axiomatiques de la mesure des aires planes.
Je vous mets le lien suivant : http://www.math.u-psud.fr/~perrin/CAPES/geometrie/trigo.pdf
A la page 6, vous pouvez voir la définition exacte de mon cours sur la mesure des aires planes.


La mesure des aires planes est tout simplement la fonction vérifiant les 4 axiones.
Cependant, je bloque déjà sur les remarques (les même sont faites dans mon poly). Pourquoi a t-on (B) = (A) + (A B) ?
De même, dans mon cours, il est dit que (AuB) = (A) + (B) - (AnB), et je ne vois pas d'où cela provient ...

[Nightmare]

Salut,

attention aux hypothèses, pour que la mesure de B soit la somme des mesures de A et de A-B, il faut supposer que . Dans ce cas c'est direct par l'hypothèse d'additivité :

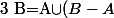et A et B-A sont disjoints donc . Essaye de réfléchir à l'autre, tout aussi facile.

[goudou]

D'accord, je te remercie.
Je suis d'accord avec toi, j'avais trouvé ça d'ailleurs. C'est dans le poly qu'ils se sont trompés, car c'est bien ;)(B) = ;)(A) + ;)(B - A) et non ;)(B) = ;)(A) + ;)(A ;) B) [ Je ne pense pas dire de bêtises, A-B et B-A, ça n'est pas la même chose !! ]
Du coup, j'ai réussi à prouver les autres égalités sans difficultés !

[goudou]

Désolée, je rebloque déjà ...

On considère maintenant un segment [AB] et C sont point milieu. Montrer que ;)([AC[)=;)([AC]) et que ;)([AB])=4;)([AC])

[Nightmare]

[AC[=[AC]-{C}, et la mesure d'un singleton est nulle !

Pour la suite, c'est l'axiome d'homogénéité : [AC] est homothétique à [AB] !

[goudou]

Ca semble pourtant évident :)

Merci beaucoup !