Question d'un dm de 1ere s
40 messages
- Page 1 sur 2 - 1, 2
question d'un dm de 1ere s
Svp, cela fait plusieurs jours que je bosse sur cette question sans trouver aucune solution ou meme debut de solution...
Soit un trapeze ABCD dont les cotes obliques se coupent en O et les diagonales en I. On se propose de demontrer en utilisant le somme de deux fonctions que la droite (OI) passe par les milieux des cotes paralleles.
Pour cela, on a muni le plan d'un repere (O,I,J) comme indiquer sur la figure si dessus, la droite (AB) etant le suport de l'axe des abscisses et l'axe des ordonnees etant paralleles a (AD).
A :
demontrer que si les droites (AC) et (BD) represente respectivement deux fonctions affines F et G alors la somme S=F+G est representer par la droite (CD).
B :
Deduire de la question A que O est le milieu de [MN] ou M et N sont les points d'intersections respectifs des droites (AC) et (BD) avec l'axe des ordonnees et que la droite (OI) represente la fonction (1/2)*S
C :
Demontrer que la droite (OI) passe par les milieux des cotes paralleles.
Soit un trapeze ABCD dont les cotes obliques se coupent en O et les diagonales en I. On se propose de demontrer en utilisant le somme de deux fonctions que la droite (OI) passe par les milieux des cotes paralleles.
Pour cela, on a muni le plan d'un repere (O,I,J) comme indiquer sur la figure si dessus, la droite (AB) etant le suport de l'axe des abscisses et l'axe des ordonnees etant paralleles a (AD).
A :
demontrer que si les droites (AC) et (BD) represente respectivement deux fonctions affines F et G alors la somme S=F+G est representer par la droite (CD).
B :
Deduire de la question A que O est le milieu de [MN] ou M et N sont les points d'intersections respectifs des droites (AC) et (BD) avec l'axe des ordonnees et que la droite (OI) represente la fonction (1/2)*S
C :
Demontrer que la droite (OI) passe par les milieux des cotes paralleles.
Bonjour,
Pour la question A :
Trouve les coordonnées de tous les points dans le repère) puis détermine les équations des droites
puis détermine les équations des droites ) et
et ) dans ce repère. Appelle-les respectivement
dans ce repère. Appelle-les respectivement 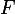 et
et 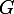 (comme indiqué) puis fais leur somme.
(comme indiqué) puis fais leur somme.
Ensuite, détermine léquation de la droite) et vérifie quelle est identique à celle de la somme de fonctions précédemment trouvée.
et vérifie quelle est identique à celle de la somme de fonctions précédemment trouvée.
Pour la question A :
Trouve les coordonnées de tous les points dans le repère
Ensuite, détermine léquation de la droite
bonjour,
tout d'abord merci d'avoir pris de ton temps pour repondre a ma question.
grace a tes indications voila ce que je trouve pour la A :
comme je n'ai pas de donnee numerique je prends des letres:
A(x1;0) B(x2;0) C(x2;y2) D(x1;y1)
equation droite (AC) : F :
(y2/(x2-x1))*x-b (b etant un nombre quelconque et x la variable)
equation droite (BD) : G :
(-y1/(x2-x1))*x+k (k etant un nombre quelconque et x la variable)
F+G=
((y2-y1)/(x2-x1))*x+k-b
equation droite (CD) :
((y2-y1)/(x2-x1))*x
ELLES SONT EGALES SEULEMENT QUAND k-b=0 ALORS QU'ELLES DEVRAIENT L'ETRE TOUT LE TEMPS.
As-tu une solution stp ?
tout d'abord merci d'avoir pris de ton temps pour repondre a ma question.
grace a tes indications voila ce que je trouve pour la A :
comme je n'ai pas de donnee numerique je prends des letres:
A(x1;0) B(x2;0) C(x2;y2) D(x1;y1)
equation droite (AC) : F :
(y2/(x2-x1))*x-b (b etant un nombre quelconque et x la variable)
equation droite (BD) : G :
(-y1/(x2-x1))*x+k (k etant un nombre quelconque et x la variable)
F+G=
((y2-y1)/(x2-x1))*x+k-b
equation droite (CD) :
((y2-y1)/(x2-x1))*x
ELLES SONT EGALES SEULEMENT QUAND k-b=0 ALORS QU'ELLES DEVRAIENT L'ETRE TOUT LE TEMPS.
As-tu une solution stp ?
Il faut dabord que tu héberges ton image sur Internet grâce à ImageShack par exemple. Tu récupères le lien « direct » quon te donne puis tu le colles dans « Texte à formater ».hetm0407 a écrit:je n'arrive pas a mettre une image sur le forum comment fait on ?
il me demande "le texte a formater", lorsque je clic sur "inserer une image... :hum:
Merci.
Y a t-il une formule pour rediger le fait que comme ils sont colineaires, (x2y1)-(y2x1)=0 ? :lol3:
J'ai reussi la question B !!! :we:
Par contre la C je ne comprend pas comment on peut prouver que la droite (OI) passe bien par le milieux des cotes paralleles... :mur:
pourrais-tu me donner juste une indication pour commencer stp
J'ai reussi la question B !!! :we:
Par contre la C je ne comprend pas comment on peut prouver que la droite (OI) passe bien par le milieux des cotes paralleles... :mur:
pourrais-tu me donner juste une indication pour commencer stp
Y a t-il une formule pour rediger le fait que comme ils sont colineaires, (x2y1)-(y2x1)=0 ? :lol3:
J'ai reussi la question B !!! :we:
Par contre la C je ne comprend pas comment on peut prouver que la droite (OI) passe bien par le milieux des cotes paralleles... :mur:
pourrais-tu me donner juste une indication pour commencer stp
Faut il :
--calculer les coordonnes des points
--utiliser les vecturs
--utiliser le cercle trigonometrique
--ou autre ?
J'ai reussi la question B !!! :we:
Par contre la C je ne comprend pas comment on peut prouver que la droite (OI) passe bien par le milieux des cotes paralleles... :mur:
pourrais-tu me donner juste une indication pour commencer stp
Faut il :
--calculer les coordonnes des points
--utiliser les vecturs
--utiliser le cercle trigonometrique
--ou autre ?
Oui c'est ça (j'espère que tu as vu ça en cours)
Pour la C
Faisons d'abord un récapitulatif
On a
(AC) : y=F(x)
(BD) : y=G(x)
(CD) : y=(F+G)(x)
M est l'intersection de (AC) et de l'axe des ordonnées. Que vaut son ordonnée ?
N est l'intersection de (BD) et de l'axe des ordonnées. Que vaut son ordonnée ?
Pour la C
Faisons d'abord un récapitulatif
On a
(AC) : y=F(x)
(BD) : y=G(x)
(CD) : y=(F+G)(x)
M est l'intersection de (AC) et de l'axe des ordonnées. Que vaut son ordonnée ?
N est l'intersection de (BD) et de l'axe des ordonnées. Que vaut son ordonnée ?
40 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


