Dm de maths barycentre

[jeanne0210]

Bonjour,

Je suis en 1ere S et j'ai un DM à faire sur les barycentres. Je ne suis pas sûre de mes réponses pour un exercice, alors si vous pouviez me les confirmer (ou pas d'ailleurs), ça serait sympa ! :++:

Ennoncé :

On considère un triangle ABC et les points I,J,K tels que : (ce sont des vecteurs)
2IB+IC=0 (vecteur nul) ; JC+2JA=0 (vecteur nul) ; KA+KB=0 (vecteur nul)

1- Placer les points I,J,K
2- Soit G barycentre de {(A;2)(B;2)(C;1)}, montrer que les droites (AI), (BJ), et (CK) sont concourantes en G.

Mes réponses :

1- 2IB+IC=0
I barycentre de {(B;2)(C;1)}
=> BI = 1/(2+1)x(BC) = 1/3 x(BC)

JC+2JA=0
J barycentre de {(A;2)(C;1)}
=> AJ= 1/(1+2) x AC = 1/3 AC

KA+KB=0
K isobarycentre de AB
=> AK= 1/2 AB

2- On a G barycentre de {(A;2)(B;2)(C;1)}
Soit H barycentre de {(A;2)(B;2)}
Ainsi G barycentre de {(H;4)(C;1)}
Or H=K, donc G appartient à (KC)

On a G barycentre de {(A;2)(B;2)(C;1)}
Soit I barycentre de {(A;2)(C;1)}
Ainsi G barycentre de {(I;3)(B;2)}
Or I=J, donc G appartient à (BJ)

Ainsi G appartient à deux médianes du triangle ABC donc les médianes sont concourantes en G.

Mes réponses me semblent bonnes pour la question 1, c'est surtout la question 2 qui me pose problème.
Merci à l'avance de votre aide ! :we:

[Jimm15]

Bonsoir,

Ça me paraît bon.

Toutefois, quand tu dis :

– « Soit H barycentre de {(A;2)(B;2)}
Ainsi G barycentre de {(H;4)(C;1)} »
Dis plutôt : « Ainsi, par associativité... »

– « Soit I barycentre de {(A;2)(C;1)}
Ainsi G barycentre de {(I;3)(B;2)} »
Même remarque.

– « Or H=K »
Précise que c’est parce que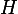 est isobarycentre de 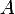et .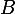

– « Or I=J »
Même remarque.

– « Ainsi G appartient à deux médianes du triangle ABC donc les médianes sont concourantes en G »
Ton raisonnement est tout à fait correct mais tu peux peut-être vérifier que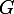 appartient bien à la droite .

[jeanne0210]

Ok ! Merci beaucoup de ton aide, alors ! :we: