Un exercice d'olympiad2

[jack01]

bonjour;
EX1
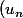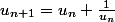
soit la suite définie par et ,pour tout n>=0;
prouver que
EX2
sachant que ;calcuer

[nodjim]

Pour passer de un=5 à 6, combien d'étapes au maximum dois tu réaliser ?

[carzou]

EX2, sans utiliser EX1

Soit A = a4+1/a4 et B = a3+1/a3
A3 = a12+1/a12 + 3A
B4 = a12+1/a12 + 6 + 4(a6+1/a6) = a12+1/a12 + 6 + 4(B2-2)

d'où
A3 = B4 - 6 - 4(B2-2) + 3A
A3-3A-103682=0 qui se factorise en
(A-47)(A2+47A+2206)=0

soit A=47

[Ben314]

Pour le 2), ça me parraissait "plus naturel" de partir dans l'autre sens, c'est à dire de poser X=a+1/a et de calculer X^3 et X^4 :
X^3=a^3+3a+3/a+1/a^3 donc X^3=3X+18 qui a comme racine "évidente" (et seule racine réelle) X=3.
X^4=a^4+4a²+6+4/a²+1/a^4 donc
a^4+1/a^4=X^4-6-4(a²+1/a²)=X^4-6-4(X²-2)=3^4-6-4(3²-2)=47

[jack01]

bien fait maitre ben314 et carzou mais pour EX1

[Ben314]

Pour le 1), nodjim as donné la "bonne indic" :
Si on sait que U_n>=x, combien de terme 1/U_k au max faut il ajouter pour être sûr que U_(n+?)>=x+1 ?
Par exemple, pour donner un (gros) indice sans tout dévoiler, on sait que U0=5 et, on peut en déduire par exemple que U10>6 car, si ce n'était pas le cas alors U0,U1,...,U9 seraient ==1/6 donc U10>=U0+10x1/6>6 : contradiction.

[jack01]

Pour le 1), nodjim as donné la "bonne indic" :
Si on sait que U_n>=x, combien de terme 1/U_k au max faut il ajouter pour être sûr que U_(n+?)>=x+1 ?
Par exemple, pour donner un (gros) indice sans tout dévoiler, on sait que U0=5 et, on peut en déduire par exemple que U10>6 car, si ce n'était pas le cas alors U0,U1,...,U9 seraient ==1/6 donc U10>=U0+10x1/6>6 : contradiction.

maitre je n'ai pas bien compris :doh: je vous demande de prendre TEX pou comprendre votre idee

[Ben314]

En réfléchissant un peu plus, il est nettement plus simple de procéder differement en constatant que la formule U(n+1)=Un+1/Un implique (U(n+1))²=Un²+2+1/Un²>=Un²+2 ce qui implique que, pour tout n et tout p, (U(n+p))²>=Un²+2p...

[jack01]

quel est la raison qui indique que "(U(n+1))²=Un²+2+1/Un²>=Un²+2 ce qui implique que, pour tout n et tout p, (U(n+p))²>=Un²+2p..."

[nodjim]

En réfléchissant un peu plus, il est nettement plus simple de procéder differement en constatant que la formule U(n+1)=Un+1/Un implique (U(n+1))²=Un²+2+1/Un²>=Un²+2 ce qui implique que, pour tout n et tout p, (U(n+p))²>=Un²+2p...

Saut de puce magistral!