Equation a résoudre

[cristelle]

Bonjour,

J'ai un petit exercice a faire celui de résoudre cette équation pour trouver le y avec des opérations simples sans avoir a faire a de gros calcules

y''= -k^2 y
y= ?

Merci pour votre aide !

[Jimm15]

Bonjour,

Il faut isoler d’un côté de l’égalité.

[lol37]

Salut,
ça doit être une équation différentielle non ?
tu poses et
tu résouds tu as deux racines complexes
la solution est de la forme ( A et B se trouvent à l'aide des conditions initiales )

[Ericovitchi]

non je ne vois pas comment il peut isoler y, c'est une équation différentielle du second ordre.

Il faut suivre la théorie de résolution des équations différentielles d'ordre 2 :
http://fr.wikipedia.org/wiki/%C3%89quation_diff%C3%A9rentielle_lin%C3%A9aire_d'ordre_deux

Le cas présent est très simple, le polynôme caractéristique a 2 racines k et -k donc les solutions sont immédiates :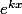 et 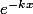qui engendrent l'espace des solutions donc

[cristelle]

je pensais a faire les intégrales pour sortir le Y non ?

[Ericovitchi]

Des intégrales :we:

Non, il faut connaître la théorie des équations différentiels du second ordre :
http://fr.wikipedia.org/wiki/%C3%89quation_diff%C3%A9rentielle_lin%C3%A9aire_d'ordre_deux

Dans ton cas le polynôme caractéristique (de donc ) a 2 racines ik et -ik. Tu es dans un cas particulier où les parties réelles sont nulles donc il reste comme l'a di lol37 :
A coskx + B sinkx.