V.a gaussienne et convergence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cam12
- Membre Naturel
- Messages: 40
- Enregistré le: 22 Avr 2010, 09:49
-
 par Cam12 » 19 Oct 2010, 21:31
par Cam12 » 19 Oct 2010, 21:31
Bonsoir, un exo classique :
Soient

des v.a indépendantes de loi gaussienne oùX_i suit une loi normale :
)
On veut étudier la convergence en loi de
X_2+.......+X_n}{n \sqrt n})
J'ai simplement fait la somme des espérances et la somme des variances et je me retrouve avec
m_2} {n \sqrt n} +.........+ \frac {m_n} {n sqrt n} ,\ \frac{\sigma _1^2}{n} + \frac {(n-1)^2 \sigma _2^2} {n^2} + ..... + \frac{\sigma _n^2}{n^3}))
J'imagine qu'il y a mieux à dire.....
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Oct 2010, 22:18
par Sylviel » 19 Oct 2010, 22:18
Une somme de gaussienne est une gaussienne. Met tout sur le même dénominateur et essaie de simplifier la somme si y'a moyen...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 19 Oct 2010, 22:24
par arnaud32 » 19 Oct 2010, 22:24
j'ai peur que la limite de ta moyenne ne diverge ...
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Oct 2010, 22:26
par Sylviel » 19 Oct 2010, 22:26
Arnaud : sans hypothèses supplémentaires sur les moyennes et les écart types on ne peux rien dire de la convergence :zen:
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Cam12
- Membre Naturel
- Messages: 40
- Enregistré le: 22 Avr 2010, 09:49
-
 par Cam12 » 20 Oct 2010, 10:04
par Cam12 » 20 Oct 2010, 10:04
Mettre tout sur le même dénominateur, je veux bien mais ca me donne quelque chose qui ne se simplifie pas.....
la moyenne vaut
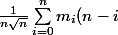)
mais ça ne m'avance pas vraiment :triste:
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Oct 2010, 10:12
par arnaud32 » 20 Oct 2010, 10:12
Sylvie a raison, sans autre hypotheses tu ne peux pas dire grand chose.
Par exemple
si m_i = 0 pour tout i, ca converge vers 0
si m_i=m non nul pour tout i alors tu as
}{2*n*\sqr{n}})
qui diverge.
-
Cam12
- Membre Naturel
- Messages: 40
- Enregistré le: 22 Avr 2010, 09:49
-
 par Cam12 » 20 Oct 2010, 10:19
par Cam12 » 20 Oct 2010, 10:19
Ok, merci....je vois. Mais je reste quand même convaincue qu'il existe une solution à cet exercice, je l'ai trouvé dans quasiment tous les cours de probas niveau M1/prépa agreg.....malheureusement je n'ai pas la correction.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Oct 2010, 10:23
par arnaud32 » 20 Oct 2010, 10:23
es tu sur de l'enonce?
-
Cam12
- Membre Naturel
- Messages: 40
- Enregistré le: 22 Avr 2010, 09:49
-
 par Cam12 » 20 Oct 2010, 10:42
par Cam12 » 20 Oct 2010, 10:42
hmmmm, désolée! Il s'agit de var centrée réduites.....autant pour moi!
Du coup la moyenne tend vers 0. Par contre pour la variance, j'ai
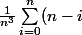^2)
qui doit se simplifier mais comment.....
Pour établir la convergence en loi, est-ce correct d'étudier seulement la convergence simple des 2 paramètres de ma gaussienne?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Oct 2010, 10:48
par arnaud32 » 20 Oct 2010, 10:48
pour calculer la somme, tu peux utiliser (n+1)²=n²+2n+1 et sommersur n des deux cotes et regarder ce que ca fait.
pour la convergence en loi, quelle en est la definition?
-
Cam12
- Membre Naturel
- Messages: 40
- Enregistré le: 22 Avr 2010, 09:49
-
 par Cam12 » 20 Oct 2010, 11:02
par Cam12 » 20 Oct 2010, 11:02
pour la variance, j'ai
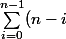^2 = \sum_i n^2 + \sum_i i^2 -2 \sum_i ni = n^3 + .....- n^2(n-1))
, je ne me souviens plus de la somme des i^2...mais je sais que c'est quelque chose équivalent à n^3 en l 'infini, au final j'ai donc ma variance qui équivaut à 1. Ma gaussienne serait donc centrée, réduite.
Pour la définition de la convergence en loi, justement je n'en ai aucune à part celle avec les espérances(on peut intervertir espérance et limite).
Dans le cas de cet exo, je vosi bien que la loi sera gaussienne et je ne vois pas comment on pourrait faire autrement pour trouver les paramètres qu'en étudiant la convergence simple mais vu que c'est nouveau, tout ça ne me parait pas évident.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Oct 2010, 11:52
par arnaud32 » 20 Oct 2010, 11:52
une suite de va X_i converge en loi vers X, si la suite des fonctions de repartion F_i des X_i converge vers la fonction de repartition de X F , en tout point de continuite de F.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Oct 2010, 12:10
par arnaud32 » 20 Oct 2010, 12:10
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Oct 2010, 12:34
par arnaud32 » 20 Oct 2010, 12:34
desole pour le brouillon je ne suis pas un pro du TEX
la fin:
(2n+1)}{6})
-
Cam12
- Membre Naturel
- Messages: 40
- Enregistré le: 22 Avr 2010, 09:49
-
 par Cam12 » 20 Oct 2010, 12:48
par Cam12 » 20 Oct 2010, 12:48
Arnaud, je ne vois pas pourquoi on utilise (n+1)^3....? Je veux sommer (n-i)^2 pour i de 0 à n-1......
-
mathelot
 par mathelot » 20 Oct 2010, 12:51
par mathelot » 20 Oct 2010, 12:51
Cam12 a écrit:j'ai
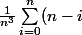^2)
qui doit se simplifier mais comment.....
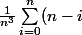^2=\frac{1}{n^3} \sum_{k=n}^{0} \, k^2=\frac{n(n+1)(2n+1)}{6n^3})
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Oct 2010, 12:51
par arnaud32 » 20 Oct 2010, 12:51
c'est juste une methode pour trouver la somme des i² qui est ton second terme dan ta variance.
-
Cam12
- Membre Naturel
- Messages: 40
- Enregistré le: 22 Avr 2010, 09:49
-
 par Cam12 » 20 Oct 2010, 17:02
par Cam12 » 20 Oct 2010, 17:02
Merci beaucoup à tous!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités