Primitive (x+3)² (TS)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
derivcompo
- Membre Naturel
- Messages: 25
- Enregistré le: 16 Oct 2010, 20:39
-
 par derivcompo » 16 Oct 2010, 20:47
par derivcompo » 16 Oct 2010, 20:47
Bonsoir,
Après avoir fait connaissance avec la notion de primitive, je m'initie à quelques calculs, mais je bloque concernant la méthode d'une composée d'apparence simple:
f (x) = (x+3)²
J'ai notée f(x) = uov (x)
u(x) = x+3 v(x) = x²
U(x) = (1/2)x² + 3x V (x) = (1/3) x^3
(avec U , V et F primitives)
d'où, en suivant mon intuition première : F(x) = (1/3) [ (1/2) x² + 3x ]^3
soit: F(x) = V ( U(x) )
Et là, j'ai un souci, car visiblement la dérivée de F(x) n'est pas égale à f(x); pouvez-vous me donner une méthode ?
Merci d'avance
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 16 Oct 2010, 20:53
par Mortelune » 16 Oct 2010, 20:53
Bonsoir.
Dans ton cas selon ce que tu as vu tu peux faire un changement de variable ou développer le carré et utiliser le fait que l'intégrale de la somme (finie) c'est la somme des intégrales.
-
derivcompo
- Membre Naturel
- Messages: 25
- Enregistré le: 16 Oct 2010, 20:39
-
 par derivcompo » 16 Oct 2010, 20:54
par derivcompo » 16 Oct 2010, 20:54
Mortelune a écrit:Bonsoir.
Dans ton cas selon ce que tu as vu tu peux faire un changement de variable ou développer le carré et utiliser le fait que l'intégrale de la somme (finie) c'est la somme des intégrales.
Merci , mais est-il possible de résoudre sans connaître la notion d'intégrale ? :hum:
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 16 Oct 2010, 21:00
par Mortelune » 16 Oct 2010, 21:00
Oui.
Tu peux essayer de regarder la dérivée de
^3)
et d'en déduire une constante multiplicative.
-
Le Chaton
- Membre Irrationnel
- Messages: 1335
- Enregistré le: 12 Oct 2008, 19:00
-
 par Le Chaton » 16 Oct 2010, 21:02
par Le Chaton » 16 Oct 2010, 21:02
Bonsoir ,
sinon tu peux développer et le faire tout simplement :p :ptdr:
-
derivcompo
- Membre Naturel
- Messages: 25
- Enregistré le: 16 Oct 2010, 20:39
-
 par derivcompo » 16 Oct 2010, 21:16
par derivcompo » 16 Oct 2010, 21:16
Mortelune a écrit:Oui.
Tu peux essayer de regarder la dérivée de
^3)
et d'en déduire une constante multiplicative.
Je trouve 3 ( x+3) ² pour la dérivée de (x+3)^3
Il semble que
^n ]' = n(mx+p)^{n-1})
, mais .... :hein:
Est-ce que ça veut dire que la primitive de
^2)
est
^2)
?
Le Chaton a écrit:Bonsoir ,
sinon tu peux développer et le faire tout simplement :p :ptdr:
Oui merci, c'est plus simple, mais j'ai du temps et c'est moins rigolo que de chercher une technique ! :happy2:
-
derivcompo
- Membre Naturel
- Messages: 25
- Enregistré le: 16 Oct 2010, 20:39
-
 par derivcompo » 16 Oct 2010, 21:45
par derivcompo » 16 Oct 2010, 21:45
:id:
Tout simplement, en posant , pour
^2, X=x+3)
Je trouve la primitive de
=(x+3)^2)
qui est
=1/3(x+3)^3)
Ce qui reviens au changement de variable. Toutefois, j'aimerais comprendre ton autre méthode, peux-tu me l'expliquer ? Merci :happy2:
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 16 Oct 2010, 21:56
par Mortelune » 16 Oct 2010, 21:56
Si tu parle de la dérivation de
^3)
alors tu as remarqué que en posant
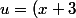^2)
(pour bien remarquer le lien que tu as écrit au dessus)
^3)'=3u)
donc qu'en divisant par 3 on avait ce qu'on voulait.
-
derivcompo
- Membre Naturel
- Messages: 25
- Enregistré le: 16 Oct 2010, 20:39
-
 par derivcompo » 16 Oct 2010, 22:01
par derivcompo » 16 Oct 2010, 22:01
Tout à fait! Merci beaucoup :+++: et bonne fin de soirée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
et d'en déduire une constante multiplicative.
