Petit probleme pour démontrer une somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kir4
- Messages: 4
- Enregistré le: 16 Oct 2010, 15:53
-
 par kir4 » 16 Oct 2010, 15:57
par kir4 » 16 Oct 2010, 15:57
Bonjour,
J'ai une question dans mon td, mais je n'arrive pas a trouver comment on fait:
L'exercice est :
Montrer que
n
E k = n(n+1)/2
k = 1
et Calculer :
n
E 2k+1
k=0
Merci de votre aide
Alex
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Oct 2010, 16:26
par girdav » 16 Oct 2010, 16:26
Bonjour,
le gros du problème est de déterminer la première somme (pour la seconde on s'aide de la linéarité).
Es-tu d'accord avec ceci :
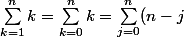=\sum_{k=0}^n(n-k))
?
-
kir4
- Messages: 4
- Enregistré le: 16 Oct 2010, 15:53
-
 par kir4 » 16 Oct 2010, 16:34
par kir4 » 16 Oct 2010, 16:34
oui, je suis d'accord avec ce que vous m'avez passé, mais je ne vois pas comment je peux montrer la suite.
Désole de ne pas savoir.
Alex.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Oct 2010, 17:20
par girdav » 16 Oct 2010, 17:20
Si tu ajoutes la deuxième et la quatrième somme qu'est-ce que tu obtiens?
-
Vortad
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Oct 2010, 15:01
-
 par Vortad » 16 Oct 2010, 17:56
par Vortad » 16 Oct 2010, 17:56
En gros il faut montrer que:
1+2+3+4+5+6... n = n(n+1)/2 si j'ai bien compris?
Le principe est celui ci:
I=1+2+3+4+5+6...n
I=n+(n-1)+(n-2)...1
tu pige?? bien, après ca, il faut additionner les deux menbres du haut et du bas, tu obtiens 2I, il suffit de diviser par 2.
-
kir4
- Messages: 4
- Enregistré le: 16 Oct 2010, 15:53
-
 par kir4 » 16 Oct 2010, 18:14
par kir4 » 16 Oct 2010, 18:14
Merci à vous deux, j'ai compris le principe.
et pour :
n
E 2k+1
k=0
" (pour la seconde on s'aide de la linéarité). "
heu .... :briques:
-
Vortad
- Membre Naturel
- Messages: 23
- Enregistré le: 13 Oct 2010, 15:01
-
 par Vortad » 16 Oct 2010, 18:34
par Vortad » 16 Oct 2010, 18:34
C'est en fait la somme des n premiers nombres impairs!
Le calcul devrait, je pense, aboutir à n^2...
Le principe est le même que pour l'exercice précédent.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Oct 2010, 18:44
par girdav » 16 Oct 2010, 18:44
kir4 a écrit:Merci à vous deux, j'ai compris le principe.
et pour :
n
E 2k+1
k=0
" (pour la seconde on s'aide de la linéarité). "
heu .... :briques:
On peut écrire que
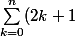 =2\sum_{k=0}^n k+\sum_{k=0}^n1)
. La première a déjà été calculée, la seconde n'est pas très dure.
-
kir4
- Messages: 4
- Enregistré le: 16 Oct 2010, 15:53
-
 par kir4 » 17 Oct 2010, 15:10
par kir4 » 17 Oct 2010, 15:10
Merci beaucoup :D
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
