Perso, à ta place, je n'écrirais pas tout les "détails" des calculs :
Lorsque
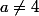
(discriminant non nul), la solution générale de l'équation

est
=\alpha e^{\lambda t}+\beta e^{\lambda't})
(

) où

et
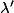
sont les deux racines (distinctes) de
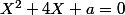
.
(le cas
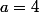
est à traiter à part).
Chercher une solution telle que
=0)
,
=0)
revient à chercher

tels que :

C'est un système linéaire qui a comme unique solution
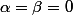
(qui donne la solution triviale

) sauf lorsque son déterminant est nul, c'est à dire lorsque
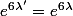
soit encore
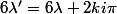
avec

(car
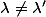
)
Il ne te reste qu'à regarder pour quelles valeurs de

l'équation
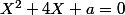
admet deux racines dont la différence est de la forme


Edit : Les trois plus petites valeurs que je trouve sont :
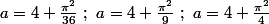
Edit 2 : je confirme ce que dit mathelot, il faut évidement rajouter "... solutions
non triviales..." dans l'énoncé !