Bonjour, je suis nouveau sur ce forum et je vous envoie ce message car je galère depuis longtemps sur un énoncé où je dois faire un raisonnement par récurrence.
L'énoncé est:
a^(n+1)-b^(n+1)=(a-b)(a^n+a^(n-1)*b+a^(n-2)*b²+....+a^(n-p)*b^p+...+b^n)
Si quelqu'un trouve la solution, ça serait vraiment sympa. :id: :id:
Merci d'avance
Raisonnement par récurrence
7 messages
- Page 1 sur 1
Oui et bien vérifies là pour n=0 ou 1 puis supposes la vraie pour n et vérifies qu'elle est encore vraie pour n+1.
L'astuce en formant c'est de l'écrire
c'est de l'écrire
(a^{n+1}-b^{n+1}) -ab (a^n-b^n)) et en te servant de la relation que tu as supposée vraie, tu vas facilement montrer que le membre de droite s'écrit (a-b) multiplié par quelque-chose.
et en te servant de la relation que tu as supposée vraie, tu vas facilement montrer que le membre de droite s'écrit (a-b) multiplié par quelque-chose.
L'astuce en formant
Salut,
Bon, l'amorce, ça consiste à montrer que la formule
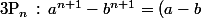(a^n+a^{n-1}b+a^{n-2}b^2+....+a^{n-p}b^p+...+b^n))
est vraie pour n=1, c'est à dire que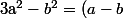(a+b)) et il me semble que c'est pas trop dur...
et il me semble que c'est pas trop dur...
Ensuite, pour la récurrence, normalement, on suppose que P_n est vraie pour un certain n et on essaye de montrer que c'est vrai pour le suivant. Ici, il faudrait arriver à écrire (qui correspond à la proposition
(qui correspond à la proposition 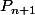 ) en fonction de
) en fonction de  (qui correspond à la proposition
(qui correspond à la proposition 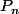 ). Sauf qu'on a beau regarder, ça parrait assez difficile.
). Sauf qu'on a beau regarder, ça parrait assez difficile.
Donc ce que propose Ericovichi, c'est de faire une récurrence double, c'est à dire de supposer que la formule est vrai pour un certain n, mais aussi qu'elle est vraie pour n-1. Dans ce cas, il faut arriver à écrire en fonction de
en fonction de  mais aussi de
mais aussi de  .
.
Et là, c'est pas trop dur :
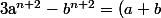(a^{n+1}-b^{n+1})-ab(a^n-b^n))
Attention tout de même que, comme on fait une récurrence double, il faut bien sûr vérifier l'amorce pour n=1 ET n=2 !
Bon, l'amorce, ça consiste à montrer que la formule
est vraie pour n=1, c'est à dire que
Ensuite, pour la récurrence, normalement, on suppose que P_n est vraie pour un certain n et on essaye de montrer que c'est vrai pour le suivant. Ici, il faudrait arriver à écrire
Donc ce que propose Ericovichi, c'est de faire une récurrence double, c'est à dire de supposer que la formule est vrai pour un certain n, mais aussi qu'elle est vraie pour n-1. Dans ce cas, il faut arriver à écrire
Et là, c'est pas trop dur :
Attention tout de même que, comme on fait une récurrence double, il faut bien sûr vérifier l'amorce pour n=1 ET n=2 !
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
