Axe de symétrie d'une courbe

[Pi.π]

On a la courbe Cf définie par f(x)=2x^2-4x+5,25. Montrer que la droite d'équation x=1 est son axe de symétrie.

[Nhalijnah]

Perso j'utiliserai la forme canonique , afin de trouver le sommet et en déduire cet axe de symétrie . Tu vois de quoi je parle ?

[Pi.π]

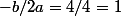
Pour le sommet, je peux simplement faire, non?

[Nhalijnah]

Simplement faire ?

[Pi.π]

Enlèves le "simplement", alors...

[Nhalijnah]

Oui , pour vérification fait attention d'avoir un discriminant = 0. B^2 - 4ac

[Pi.π]

Le discriminant est -2...

[Nhalijnah]

Je trouve : A=2. B= -4. C=5.25. D=. (-4)^2 - 4 * 2 * 5.25 = -26

[Pi.π]

Ça reste négatif.

[Nhalijnah]

Donc tu as deux intersections avec l'axe des abscisses , donc ta formule est inutilisable . Je reste sur la position de la forme canonique

[Nhalijnah]

Pas d'intersections pardon

[Pi.π]

D'accord. Merci. Et la forme canonique? Comment on fait?

[Pi.π]

J'ai trouvé 2[(x+1)^2-3,25/2]

[Nhalijnah]

Tu ne l'as pas vu ? 2x^2 - 4x + 5.25. 2(x^2 - 2x + 2.625). 2(x^2 - 2*1*x + 2.625). Donc = 2 (x^2 - 2*1*x +1^2 + 2.625 - 1^2). (Identités remarquables). Cela donne = 2((x-1)^2 + 1.625). Tu lis donc x-1=0 d'où x=1 ce qui te donne l'abscisse de ton sommet , rt l'ordonnee qui est 2*1.625. Désole de la lenteur depuis i phone c'et long

[Pi.π]

Ah ouais, d'accord!
Je te comprends. Je suis sur mon iPad, c'est le même problème.

[Nhalijnah]

Hihi , j'ai pi t'aider c'est bon ?

[Pi.π]

Mais comment je peux l'écrire ça?
Je dis que si la courbe Cf a un axe de symétrie, il passe par son sommet. J'expose la forme canonique, je dis que l'abscisse du sommet est 1 et que sa colle avec?

[Pi.π]

Où est la droite d'équation x=1, évidement.

[Nhalijnah]

Bahvqur l'axe de symétrie de ta courbe coupe la courbe en son sommet donc x=1 ,

[Pi.π]

Merci beaucoup!