Séries suites

[Jfmamjjasond2]

Hello,

Pour , on pose

1. Prouver que la suite converge vers 1.
2. Déterminer la nature de la série

Au début je m'étais dit que ce serait simple en mettant ça sous la forme et en utilisant les DL sauf que ça ne marche pas (cos tend vers 1 en 0...)
Et la question 2 je n'y arrive pas plus.

Vous avez quelques pistes svp ? J'ai honte de galérer là dessus. Cet exercice est le 1er de ma feuille de TD...

Merci d'avance pour votre aide.

[Ericovitchi]

Oui développement limité de la fonction (1-cosx)^tanx au voisinage de 0 est la solution standard pour étudier la limite.
~ e^tan x (ln (1-cos x) etc... on trouve 1 comme limite car 1-cos x ~ x²/2 , et x lnx tends vers 0 quand x tends vers 0 et donc l'exponentielle tends vers 1

en fait (1-cosx)^tanx ~ 1+2xlnx ça peut servir pour la question 2)

[windows7]

salut,

pose Vn=ln((1-cos(1/n)) * sin(1/n)*(cos(1/n))

Wn= V1*.. Vn

quelle est la limite de W ?

[Jfmamjjasond2]

On peut composer un équivalent à gauche par ln même quand la limite est 0 ?

[Jfmamjjasond2]

Re,

J'ai réussi l'exercice grâce à vos conseils et j'ai pu avancer sur ma feuille de TD. Mais maintenant je galère plus loin :

Soit une suite d'éléments de une suite réelle telle que :



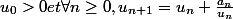
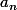
Démontrer que la suite converge si et seulement si la série converge.

J'ai commencé par faire le raisonnement suivant :
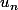
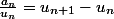
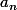
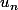
si converge, alors converge et, de plus, converge et donc que converge (car ). Il me faut maintenant montrer que converge si on a que converge et que converge aussi. En fait je ne sais même pas si c'est vrai. Je ne sais pas non plus si je peux remplacer mes "donc" et "si alors" par des "ssi".

Suis-je sur la bonne voie ou pas ?

Merci d'avance pour votre aide encore une fois.

[Pythales]

Une explication osée :
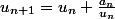
s'écrit

soit en continu

soit en intégrant :

Il est clair que tend vers une limite si l'intégrale converge,
et on sait que la convergence de l'intégrale est liée à celle de la série

[Ericovitchi]

ha oui, ça c'est osé, mais effectivement c'est super bien vu comme approche.
j'étais justement en tain de chercher et de faire des sommes en me disant que c'était dommage que ça ne soit pas continu parce que ça ressemblait à des sommes de Riemann.

[Ben314]

Salut,
Une méthode "moins osée" :

- Si Un tend vers L alors an=Un(U(n+1)-Un)=
- Comme la suite Un est croissante, on a Un=>U0 pour tout n donc
U(n+1)=Un=et donc que, si la série des an est C.V. alors la suite Un est majorée donc convergente.