Dm Ts

[lucas59179]

Sn = a (1 - qn ) / (1 - q ) ? :) ( j'ai beau avoir la formule ... je suis toujours nul XD )

[Rebelle_]

Oui alors il faut préciser quelques petites choses !

Cette formule de la somme n'est valable que si la raison est différente de 1 (si non, S = N*P avec les notations que je vais donner).
Plus simplement, on a S = (P*(1-q^N)) / (1-q) avec S la somme, P le premier terme et N le nombre de termes.
Peux-tu l'appliquer ici ?

[lucas59179]

Euh je vais essayé de l'appliqué S= ( (b-a)(1/2)^n(1-(1/2)^n)) / ( 1 -1/2 ) = ?

[Rebelle_]

C'est presque ça sauf qu'il y a quelque chose en trop !
S = ((b-a) (1-(1/2)^n)) / (1 - 1/2), on ne peut pas aller beaucoup plus loin sauf à simplifier le denominateur. Le but ensuite est de remarquer le lien entre cette somme et l'expression donnée dans l'énoncé de u_{n+1} en fonction de u_n et de u_{n-1}...

[lucas59179]

( C'est ca le soucis des maths à mes yeux y a trop de complications et de soucis d'applications dans les formules :( )
Je vois pas ce que tu veux dire :s

[Rebelle_]

Eh bien je veux dire que ton énoncé demande de déduire de cette somme le terme général de (u_n).

Dans les faits je pourrais donner l'expression de (u_n) en fonction de n mais je ne saurais pas le justifier très rigoureusement (en fait je passe par l'équation caractéristique de la suite).
Donc là, il faut trouver une technique, une astuce pour exprimer (u_n) en fonction de n mais je n'ai malheureusement pas encore trouvé laquelle était-ce =P

Je vais réfléchir à ce petit problème et je te dirai quand j'aurai une piste. D'ailleurs si quelqu'un d'autre a une idée... ^^'

[lucas59179]

Donc on peut pas trouver? :(

[Ericovitchi]

il faut écrire les équations les unes en dessous des autres :


------------


____________________________________________
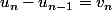
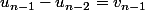
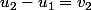
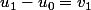
et toutes les ajouter membre à membre. Tous les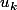 se simplifient sauf le premier et le dernier donc on trouve que


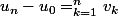
voilà le lien. Comme tu as déjà brillamment trouvé la somme des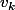 ça va te donner

[lucas59179]

c'est à dire ? ( je ne comprend pas )

[lucas59179]

STP Eicovitchi explique moi pour la q2 et q3 sinon j'y arriverais pas :(

[Ericovitchi]

Rebelle t'a donné la solution de la 2 dans son post #18 et moi je t'ai donné la solution de la 3.
Qu'est-ce que tu ne comprends pas. Commences par lire les explications aussi.

[lucas59179]

Dans le post 18 c'était pour la question 1

[lucas59179]

Dans ton post 28 ... je ne vois pas où tu veux en venir ...