J'ai bien essayé de montrer que cos(n
Et merci.
Cosinus
3 messages
- Page 1 sur 1
cosinus
par ger-00-der » 05 Oct 2010, 00:30
Bonjour,
J'ai bien essayé de montrer que cos(n
) est un polynôme en cos(), mais je n'arrive pas, pouvez-vous m'aider???
Et merci.
J'ai bien essayé de montrer que cos(n
Et merci.
par Ben314 » 05 Oct 2010, 09:12
Salut,
Si tu as vu les nombres complexes, une autre méthode trés trés classique est d'écrire que :
\ <br />=\ {\rm Re}\big(e^{in\alpha}\big)\ <br />=\ {\rm Re}\Big(\big(e^{i\alpha}\big)^n\Big)\ <br />=\ {\rm Re}\Big(\big(cos(\alpha)+i\sin(\alpha)\big)^n\Big)\ <br />=\ {\rm Re}\Big(\sum_{k=0}^n{ n\choose k}i^k<br /> \sin^k(\alpha)\cos^{n-k}(\alpha)\Big))
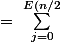}{ n\choose 2j}(-1)^j<br /> \sin^{2j}(\alpha)\cos^{n-2j}(\alpha)\ <br />=\ \sum_{j=0}^{E(n/2)}(-1)^j { n\choose 2j}<br /> \big(1-\cos^2(\alpha)\big)^j\cos^{n-2j}(\alpha))
Si tu as vu les nombres complexes, une autre méthode trés trés classique est d'écrire que :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :