Matrice diagonalisable?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
megurine_luka
- Membre Naturel
- Messages: 45
- Enregistré le: 04 Sep 2010, 11:37
-
 par megurine_luka » 04 Oct 2010, 17:41
par megurine_luka » 04 Oct 2010, 17:41
BONSOIR,
Je n'arrive pas la question 2 de l'ex suivant,
 \in IR^n et (b_1,b_2,...b_n)\in R^n, J=[a_ib_j]\\ \\ \\ 1)Calculer J^n (pour n \in N)) 2) J est-elle diagonalisable?
2) J est-elle diagonalisable?
1) en notant A et B les vecteurs lignes
\ ;\ B=(b_1,b_2,...b_n))

J est une matrice n

n dont l'élément courant

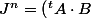^n =\,{}^t A \cdot\left(B \cdot {}^tA \right)^{n-1} \cdot B)
2) comment puis-je montrer que J est diagonalisable?
Merci
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Oct 2010, 18:06
par girdav » 04 Oct 2010, 18:06
Bonjour,
je pense que l'on peut simplifier la formule pour la question 1). Si on calcule par exemple le terme
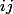
de
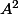
(en notant

le terme général de

) on obtient que
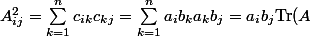)
donc on voit que
 A)
.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 04 Oct 2010, 18:51
par Skullkid » 04 Oct 2010, 18:51
Bonsoir, que peux-tu dire du polynôme minimal de J ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Oct 2010, 15:10
par yos » 05 Oct 2010, 15:10
megurine_luka a écrit: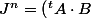^n =\,{}^t A \cdot\left(B \cdot {}^tA \right)^{n-1} \cdot B)
2) comment puis-je montrer que J est diagonalisable?
Le facteur central
^{n-1})
est un scalaire

donc tu as
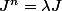
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités