[MPSI] Produit scalaire, équivalences.

par **Iris19** » 02 Oct 2010, 17:39

Bonsoir,

Je bloque sur la seconde partie de mon DM depuis un bon moment, c'est pourquoi je viens ici dans l'espoir que vous puissiez m'apporter une petite aide...

Voilà mon énoncé :

Dans le plan rapporté à un repère orthonormé d'origine O, on considère un cercle C de centre O et de rayon R > 0.
Soient P et Q deux points tels que OP > R et OQ > R.
Soient U et V les points de C tels que P = M(U,V) soit l'intersection des tangentes à C en U et V, et U', V' ceux tels que Q = M(U',V').
Établir l'équivalence des conditions suivantes :
(i) (vecteur OP).(vecteur OQ) = R²
(ii) U, V, Q alignés
(iii) U', V' P alignés

Voilà, un grand merci d'avance pour toute aide !

par **Doraki** » 02 Oct 2010, 18:31

Tu as fait un dessin ? tu penses quoi des droites (OP) et (UV) ?

par **Dinozzo13** » 02 Oct 2010, 18:39

Que signifie P = M(U,V) ?

par **Iris19** » 02 Oct 2010, 18:49

Dinozzo, oui j'ai fait un dessin et apparemment (OP) est orthogonale à (UV). Mais cela me semble difficile à prouver, et surtout, je ne comprends pas trop le rapport..

Doraki, P = M(U,V) est l'intersection des tangentes à C en U et V. Désolée, je voulais reformuler mon énoncé et je me suis mal exprimée.

par **Doraki** » 02 Oct 2010, 19:03

Ben commence par le prouver.

C'est important, parceque l'ensemble des points Q tels que OP.OQ = r², c'est un ensemble de points qui est une certaine droite qui est forcément perpendiculaire à (OP).

par **Iris19** » 02 Oct 2010, 19:14

D'accord, je le démontrerai.

Mais je ne vois pas à quoi cela aboutira. Je ne dois pas chercher l'ensemble des points tels que OP.OQ = R² ; je dois prouver que OP.OQ = R² <=> U, V, Q alignés <=> U',V',P alignés...

par **Ben314** » 02 Oct 2010, 20:06

Iris19 a écrit:D'accord, je le démontrerai.

Mais je ne vois pas à quoi cela aboutira. Je ne dois pas chercher l'ensemble des points tels que OP.OQ = R² ; je dois prouver que OP.OQ = R² U, V, Q alignés U',V',P alignés...

Sauf que montrer que
OP.OQ = R² U, V, Q alignés ,
ben ça revient trés précisément (et trés exactement) à montrer que l'ensemble des points tels que OP.OQ = R² est la droite (UV) !!!!

par **Iris19** » 02 Oct 2010, 20:27

Oui mais il n'y a aucune variable ici, O, P, Q et R sont fixés ! Je ne comprends pas de quel ensemble de points on parle.. !

par **Doraki** » 02 Oct 2010, 20:35

Ah ? Il vaut combien R ?

par **Iris19** » 02 Oct 2010, 20:40

Ben on sait simplement qu'il est strictement positif, mais il me semble qu'il n'est pas variable.

par **Doraki** » 03 Oct 2010, 12:12

Si P et Q n'étaient pas variables, ça voudrait dire qu'on t'aurait donné un dessin avec tous les points déjà placés. (ou alors on t'aurait dit précisément où ils étaient).
Et tu aurais juste à constater sur le dessin si oui ou non U,V,Q sont alignés, si U',V',P sont alignés, et si OP.OP = r², et vérifier que tu as la même réponse à chaque question.

Mais dans ton problème, P et Q sont variables, et tu dois montrer que les configurations où U V et Q sont alignés sont exactement les configurations où OP.OQ = r², etc.

par **Iris19** » 03 Oct 2010, 15:57

Ok, je vois. Mais comment procéder ? Une piste ? Ça fait des jours que je bloque...

par **Ben314** » 03 Oct 2010, 16:11

Ben, "une piste", Doraki t'en a donnée une (et une bonne...) :
Tu devrais savoir quel est l'ensemble des solutions d'une équation de la forme

(A point connu,U vecteur non nul connu, k réel connu) et tu utilise ça pour en déduire la nature de l'ensemble des points Q tels que

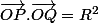
(pour O,Q et R fixés)...

par **Iris19** » 03 Oct 2010, 17:16

Mh.. Non, j'ai beau retourner mon cours dans tous les sens, je ne connais pas l'ensemble des solutions de AM.u = k.

Je n'ai que la ligne de niveau MA.MB = k, qui me donne soit un cercle, soit l'ensemble vide.

par **Doraki** » 03 Oct 2010, 17:51

Même pour quand k = 0 ?

par **Iris19** » 03 Oct 2010, 17:55

Non, pour k = 0, je sais que cela signifie que AM et u sont colinéaires.

Mais pour le restant des k...

par **Iris19** » 03 Oct 2010, 17:55

AM et u sont orthogonaux *

Petit lapsus, désolée.

par **Doraki** » 03 Oct 2010, 18:01

Si tu trouves un point P tel que AP.u = k,
alors les points M tels que AM.u = k sont les points M tels que PM.u = (AM-AP).u = AM.u - AP.u = k-k = 0.

par **Iris19** » 03 Oct 2010, 18:17

Oui, mais lorsque l'on parle de AM.u, on a A et u qui sont connus.
Or, dans OP.OQ = R², P et Q ne sont pas connus.

Je ne comprends pas le rapport, ni comment utiliser la relation que tu cites.. !

par **Ben314** » 03 Oct 2010, 18:58

L'idée, c'est uniquement de considérer que O,P,U,V sont fixés (on sait pas où ils sont précisément, mais nous, dans tout le raisonnement que l'on va tenir, ils seront toujours au même endroit).
Par contre, Q, lui, on imagine qu'il "bouge" et on veut montrer qu'il est situé sur la droite (UV) ssi OP.OQ=R².
Or, tu vient de voir (ça m'étonne que tu ait vu l'équation AM.BM=k sans avoir jamais vu AM.u=k qui est plus simple, mais bon...) que l'ensemble des points Q tels que OP.OQ=R² est une droite. Pour montrer que c'est la droite (UV) il suffit donc de montrer que U et V vérifient l'équation en question (en fait un seul des deux peut suffire vu qu'on sait que la droite en question est perpendiculaire à (OP)).

[MPSI] Produit scalaire, équivalences.

[MPSI] Produit scalaire, équivalences.

Qui est en ligne