Suites

[polka-dots]

Bonjour,

J'ai une suite de la forme Un+2 = aUn+1 + bUn.
On considère E, l'ensemble des solutions de cette "équation". E est un R-ev, et j'ai:

phi: E-> R²
(Un)n -> (U0,U1)

Je ne comprends pas les démonstrations pour phi surjective, et phiinjective.

Pour phisurjective, quelquesoit alpha,beta appartient R², ilexiste(Un)n appartient E telle que u0=alpha et U1=beta. Je ne vois pas comment ici on a pu démontrer qu'elle était surjective?

De même pour phi injective,

u0=u1=0 => quelquesoit n, Un=0 (par récurrence). Pourquoi ici phi est injective?

[benekire2]

Salut

Ce que je ne comprends pas dans ce que tu as dit c'est que la démo de ta question est dans tes phrases ...

Il est facile de vérifier que le noyau de ton application est la suite nulle. En effet comme tu l'as si bien dit si u0 et u1 valent 0 et bien un=0 pour tout n ... ça ne te suffit pas ?

Sinon, pour la surjectivité, quelque soit (a,b)€R² on trouve une suite telle que u0=a et u1=b

Mais tu n'as même pas besoin de la surjectivité pour montrer que c'est un isomorphisme, l'injectivité (ou la surjectivité au choix) suffit.

[polka-dots]

ah d'accord, ok j'ai compris. J'ai une autre question:

J'ai l'équation caractéristique (qui découle de la relation de récurrence, en posant un= r^n):

r² - ar - b = 0.

Dans le cas où le discriminant est positif, j'ai 2 racines réelles. ,

j'ai et pour r2, j'ai la même chose. Ca vient d'où?

De même, dans le cas où le discriminant est négatif, j'ai: Un=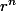 , 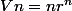(d'où est-ce que ça vient Vn??)

J'ai: Comment obtient-on ces matrices colonnes? merci

[benekire2]

Re, ici en fait, r1^0=1 et r1^1=r1 rien de plus, la notation en colone est la même que si t'était en ligne, i.e dans R² comme tout à l'heure.

[polka-dots]

Ok, et pour la suite Vn = nr^n? Elle sort d'où?
Et comment trouve-t-on Un= r^n( lambda + nµ) pour un discriminant nul?

[Ben314]

Salut,
Attention, la suite n.r^n n'est utile QUE lorsque le discriminant de r² - ar - b = 0 est nul.
En fait, quand la discriminant est strictement négatif, l'équation adme deux racines distinctes complexes r1 et r2 et on peut quasi recopier le cas delta>0 .
Un problème se pose lorsque le discriminant est nul car on n'a plus qu'une solution "élémentaire" Un=r^n alors que l'on sait que l'espace vectoriel est de dimension 2. Dans ce cas (Delta=0) et uniquement dans ce cas, on vérifie trés aisément que, non seulement la suite An=r^n est un élément de E, mais que la suite Bn=n.r^n est aussi un élément de E (fait toi même la vérification). C'est impeccable : on a deux élément de E qui sont libres (à vérifier) et E est de dimension 2 donc tout les autres éléments de E sont de la forme Un=alpha.An+beta.Bn=(alpha+beta.n)r^n avec alpha et beta deux réels.