Exercice term S asymptotes et symetrie

[mayofficial]

Bonjour à tous !
j'ai un exercice de dm qui me pose quelques soucis.
j'ai f(x) = -2x^2+6x-3 /(x-2) (courbe C)
je trouve 2 asymptotes :
-verticale x=2
-oblique y= -2x+2
j'ai trouvé le point A (2;-2) intersection de mes 2 asymptotes

mais après je dois démontrer que pour tout point M (sur la courbe C) son symétrique M' par rapport à A est un point de C et je n'ai aucune idée de comment procéder.
Si quelqu'un pouvait me donner une piste ce serai super.
Merci d'avance !

[Ericovitchi]

tu écris que
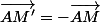
en remplaçant par les coordonnées de M'(x',y') et celles de M(x,y) ça va te donner des formules x' et y' fonction de x,y ou réciproquement

Après tu remplaces dans ton équation y=f(x) les x et y fonction de x' et y' et tu montres que tu as bien aussi y'=f(x')

[mayofficial]

je ne comprend pas ^^
j'ai x'-2 = 2-x
et y' + 2 =-2 -y
C'est ça ?

j'obtiens x'=4-x et y'= -4 -y

apres que dois je faire ? remplacer x par 4-x dans ma fonction de départ ?

[Ericovitchi]

x'=4-x et y'= -4 -y oui OK

oui tu prends y = -2x^2+6x-3 /(x-2) tu remplaces x par 4-x' et y par -4-y' et il faut que tu trouves la même équation mais y'=f(x') pour montrer que le point M' est bien sur la courbe

[mayofficial]

merci beaucoup !!!!
j'ai dit f(x')= y' =....
je fais le calcul et je retombe bien sur y= -2x^2+6x-3 / (x-2)
Dernière question : cela suffit il à prouver que M' est sur la courbe ?
merci encore de tes réponses rapides

[Ericovitchi]

si tu pars de M' et que tu montres que ça entraîne que M est aussi sur la courbe ça marche aussi. Ca démontre bien que le point A est centre de symétrie