Limite d'une fonction trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 14 Avr 2006, 21:27
par Sora » 14 Avr 2006, 21:27
Lim (sinx-x)/x^3 lorsque x tend vers 0
et merci :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Avr 2006, 07:07
par Zebulon » 15 Avr 2006, 07:07
Bonjour,
es-tu au lycée ou en sup?
A bientôt,
Zeb.
-
Anonyme
 par Anonyme » 15 Avr 2006, 14:48
par Anonyme » 15 Avr 2006, 14:48
Ah je suis pas peu fière de ma trouvaille là :we:
 \le 1)
-x \le 1-x)
-x}{x^3} \le \frac{1-x}{x^3})
Or:
=\lim_{x\rightarrow 0^-}(\frac{1}{x^3}))
(limite d'une fraction rationnelle)
=- \infty)
(car en
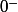
,

tend vers
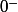
)
Enfin, comme
-x}{x^3} \le \frac{1-x}{x^3})
, par comparaison de limite, on en déduit donc que:
-x}{x^3})=- \infty)
=- \infty)
De plus,
=\frac{sin(x)-x}{x^3})
.
Donc
=\frac{sin(-x)-(-x)}{(-x)^3})
=\frac{-sin(x)+x}{-x^3})
=\frac{-(sin(x)-x)}{-x^3})
=\frac{sin(x)-x}{x^3})
=f(x))
On en déduit donc que f(x) est paire.
Or, comme
=- \infty)
. De par la parité de f(x), on en déduit que:
=- \infty)
Ainsi:
=- \infty)
:we:
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 14:51
par Sora » 15 Avr 2006, 14:51
Oui.Alors...t'as trouvé la réponse?
-
Anonyme
 par Anonyme » 15 Avr 2006, 15:07
par Anonyme » 15 Avr 2006, 15:07
Ah je suis pas peu fière de ma trouvaille là :we:
Travaillons tout d'abord sur l'intervalle
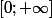
 \le 1)
-x \le 1-x)
-x}{x^3} \le \frac{1-x}{x^3})
(car

supérieur à 0 sur
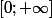
)
Or:
=\lim_{x\rightarrow 0^-}(\frac{-x}{x^3}))
(limite d'une fonction rationnelle)
=\lim_{x\rightarrow 0^-}(\frac{-1}{x^2}))
=-\infty)
(car x² tend vers

en 0)
Enfin, comme
-x}{x^3} \le \frac{1-x}{x^3})
, par comparaison de limite, on en déduit donc que:
-x}{x^3})=- \infty)
=- \infty)
De plus,
=\frac{sin(x)-x}{x^3})
.
Donc
=\frac{sin(-x)-(-x)}{(-x)^3})
=\frac{-sin(x)+x}{-x^3})
=\frac{-(sin(x)-x)}{-x^3})
=\frac{sin(x)-x}{x^3})
=f(x))
On en déduit donc que f(x) est paire.
Or, comme
=- \infty)
. De par la parité de f(x), on en déduit que:
=- \infty)
Ainsi:
=- \infty)
:we:
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 15:18
par Sora » 15 Avr 2006, 15:18
Tu as fait une grossière erreur.Lim (1-x)/x^3 lorsque x tend vers 0+ est +l'infinie
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 15 Avr 2006, 15:19
par rene38 » 15 Avr 2006, 15:19
Bonjour
-Nico- a écrit:Ah je suis pas peu fière de ma trouvaille là :we:

Dommage !
Un développement limité de sin(x) à l'ordre 5 au voisinage de 0 donne de façon immédiate :

Mais on n'est déjà plus au lycée ...
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 15:20
par Sora » 15 Avr 2006, 15:20
Zebulon et Nico...avez vous trouvez la réponse?
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 15:24
par Sora » 15 Avr 2006, 15:24
Non...la réponse est 0...On peut prendre une valeur approché de 0 et on calcule l'image de ce dernier par la fonction f(x)=(sinx-x)/x^3 puis on trouve une valeur approché de 0.seulement...il faut la démontrer théoriquement.
Aidez moi SVP a resoudre ce problème :triste:
-
Anonyme
 par Anonyme » 15 Avr 2006, 15:29
par Anonyme » 15 Avr 2006, 15:29
Mea Culpa :triste:
D'une part j'ai fait une connerie, d'autre part ma calculatrice était en degré ce qui m'a induit en erreur...
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 15:32
par Sora » 15 Avr 2006, 15:32
C'est po grave...tu peux me proposer un encadrement pour la fonction sur un intervalle de la forme ]0,a[ ?
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 15:33
par Sora » 15 Avr 2006, 15:33
ça peux nous aider...
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 15 Avr 2006, 15:33
par rene38 » 15 Avr 2006, 15:33
Sora a écrit:Non...la réponse est 0...
MuPad n'est pas d'accord :

-
Anonyme
 par Anonyme » 15 Avr 2006, 15:41
par Anonyme » 15 Avr 2006, 15:41
Sora a écrit:C'est po grave...tu peux me proposer un encadrement pour la fonction sur un intervalle de la forme ]0,a[ ?
Vi sur les positifs on a:
-x}{x^3} \le \frac{1-x}{x^3})
Et dans les négatifs on a:
-x}{x^3} \le \frac{-1-x}{x^3})
-
Anonyme
 par Anonyme » 15 Avr 2006, 15:44
par Anonyme » 15 Avr 2006, 15:44
rene38 a écrit:MuPad n'est pas d'accord :

M'enfin la, contre toute logique, ton MuPad affiche également que
-1}{1}=0)

-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 15:44
par Sora » 15 Avr 2006, 15:44
La fonction n'est pas définie en 0
désolé...
-
Sora
- Membre Naturel
- Messages: 25
- Enregistré le: 14 Avr 2006, 21:20
-
 par Sora » 15 Avr 2006, 15:46
par Sora » 15 Avr 2006, 15:46
Et puis,sin1-1/1^3=0 c'est faut!!!
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Avr 2006, 15:57
par Zebulon » 15 Avr 2006, 15:57
Moi j'ai trouvé -1/6 comme limite grâce à un développement limité de sin à l'ordre 3. Mais tu ne m'as pas répondu, es-tu au lycée ou en sup?
Zeb.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 15 Avr 2006, 16:01
par rene38 » 15 Avr 2006, 16:01
-Nico- a écrit:M'enfin la, contre toute logique, ton MuPad affiche également que


Pas du tout : regarde bien la graduation de l'axe des ordonnées : ce n'est pas l'axe des abscisses qui est visible mais la droite d'équation y=(sin(1)-1)/1 soit environ y=-0,158...
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 15 Avr 2006, 16:27
par Mikou » 15 Avr 2006, 16:27
bon sang c'est la troisieme fois que je le repete tu n'as qua encadre f sur ]0;1[ ( par ex ) par les polynome suivant
x²-1/6 et -x²-1/6 tu n'as qua demontrer linégalité verifier par les fonction et conclure avec le th des gendarmes ... bref tu fais comme tu veux mais ne vien pas te plaindre que l'on taide pas !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
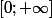
 \le 1)
-x \le 1-x)
-x}{x^3} \le \frac{1-x}{x^3}) (car
(car  supérieur à 0 sur
supérieur à 0 sur 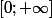 )
)=\lim_{x\rightarrow 0^-}(\frac{-x}{x^3})) (limite d'une fonction rationnelle)
(limite d'une fonction rationnelle)=\lim_{x\rightarrow 0^-}(\frac{-1}{x^2}))
=-\infty) (car x² tend vers
(car x² tend vers  en 0)
en 0)-x}{x^3} \le \frac{1-x}{x^3}) , par comparaison de limite, on en déduit donc que:
, par comparaison de limite, on en déduit donc que:-x}{x^3})=- \infty)
=- \infty)
=\frac{sin(x)-x}{x^3}) .
.=\frac{sin(-x)-(-x)}{(-x)^3})
=\frac{-sin(x)+x}{-x^3})
=\frac{-(sin(x)-x)}{-x^3})
=\frac{sin(x)-x}{x^3})
=f(x))
=- \infty) . De par la parité de f(x), on en déduit que:
. De par la parité de f(x), on en déduit que:=- \infty)
=- \infty)




