Relation d ordre

[yutor]

Bonjour,

Juste une petite question : :we:

Si j'ai une relation R réflexive symétrique et transitive sur un ensemble E , je sais que l'on peut construire un espace quotient E/R;

Mais si j'ai une relation d'ordre (cad réflexive antisymétrique et transitive) peut-on alors de la même façon construire un espace quotient et si c'est possible a-t-on alors les mêmes résultats que pour une relation d'équivalence(
je pense à la factorisation canonique des morphismes...).

MERCI POUR VOS REPONSES :we:

[Anonyme]

Salut,

Ca n'a pas beaucoup de sens car la donnée d'un ensemble quotient (i.e une partition) est exactement la même chose que se donner une relation d'ordre.

Et de toute façon, à part peut-être le cas d'une relation d'ordre totale, je vois pas comment tu définierais E/R.

[yos]

Salut,

Ca n'a pas beaucoup de sens car la donnée d'un ensemble quotient (i.e une partition) est exactement la même chose que se donner une relation d'ordre.

Et de toute façon, à part peut-être le cas d'une relation d'ordre totale, je vois pas comment tu définierais E/R.

"relation d'équivalence (ligne 3).

[Zebulon]

Bonsoir,
merci Yos, ça m'éclaire!! Je ne comprenais pas comment une partition était la même chose que se donner une relation d'ordre et pas une relation d'équivalence.
J'ai cru n'avoir rien compris aux ensembles quotient!
Zeb.

[Anonyme]

d'Equivalence bien sûr ...

[serge75]

La relation d'équivalence est intimement attachée à la notion de partition.

Par contre, pour la relation d'ordre imaginons qu'on veuille procéder de la même manière en appelant classe de x l'ensemble des éléments y tels que x précède y pour cette relation. La simple analyse de la classe de 0 dans R pour la relation usuelle nous montre qu'on obtiendrait [0,+infini[, alors que la classe de 1 serait [1,+infini[ : ces ensembles sont distintcs et non d'intersection vide : l'ensemble des 'classes' ne constitue pas une partition.
On pourrait aussi imaginer la classe de x comme l'ensemble des y qui sont comparables à x, cad tels que x précède y ou y précède x. Dans le cas d'une relation d'ordre total, on obtiendrait une seule classe, l'ensemble entier, ce qui présente peu d'intérêt. Dans le cas d'un ordre partiel, regardons l'ensemble A des parties de {1,2}, muni de l'inclusion. La classe de {1} serait : {vide,{1},{1,2}} et celle de {2} serait {vide,{2},{1,2}} : là encore ces deux classes sont distinctes mais non disjointe : on ne constitue pas une partition.

Pour aller plus loin, je te soumets la notion suivante :
On appelle préordre toute relation p réflexive et transitive. On notera xpy pour dire que x est en relation avec y par p.
Si p est un préordre, on défini la relation d'équivalence R par : xRy lorsque (xpy et ypx). R est alors une relation d'équivalence (vérification immédiate), et on définit sur E/R la relation suivante : la classe de x (notée cl(x)) précède la classe cl(y) lorsque xpy. Montrer alors que cette définition est légitime, ou en d'autres termes qu'elle ne dépend pas du représentant choisi dans cl(x) et cl(y) : si cl(x)=cl(x') et cl(y)=cl(y'), alors il y a équivalence entre xpy et x'py'. Prouver alors que précède est une relation d'ordre sur E/R.

Commentaire :
Une relation d'équivalence sert à rendre égales des quatités qui ne le sont pas. Je m'explique : réflexivité, symétrie, transitivité sont des propriétés naturellement attachées à l'égalité. Toute relation vérifiant ces trois propriétés constitue une sorte d'égalité modulo un certain critère. Prenons la congruence modulo 3 dans Z : si je suis dans un problème d'arithmétique où il s'agit de déterminer un reste par la division par trois. Vis à vis de ce problème, 2 et 5 sont identiques, bien que non égaux. La congruence me permet de dire qu'ils sont égaux vis à vis de ce problème. Mais plus fort : là où je n'ai pas égalité, et où je remplace le mot égal par le mot congru, j'ai égalité des classes : en d'autres termes, la classe de 2 et la classe de 5 sont égales.
Pour l'exercice sur les préordre que je t'ai filé, que manque-t-il à un préordre pour être une relation d'ordre : l'antisymétrie. Le préordre autorise des éléments distincts à vérifier xpy et ypx. Regroupons de tels éléments dans une même classe, de sorte à les rendre 'égaux'. Ma relation p devient d'un coup antisymétrique et c'est une relation d'ordre. Sauf que ma relation p n'est plus définie sur l'ensemble E mais sur l'ensemble quotient E/R, et change du coup de nom (je l'ai appelée précède), mais j'ai réussi mon coup : en rendant égaux des éléments qui ne l'étaient pas, j'ai transformé mon préordre p en relation d'ordre, notée précède.

En espérant t'avoir éclairci les idées sur la finalité des reations d'équivalences.
N'hésite pas à me demander d'autres exemples de 'passages au quotients'.
Serge

[sept-épées]

Salut,

il me semble qu'étant donnée une relation d'ordre sur un ensemble E, on peut définir une relation d'équivalence par quelque chose comme , c'est à dire : x et y sont en relation s' il y a un élément de E comparable à la fois à x et à y. Ce qui partagerait l'ensemble E en "fibres" pour la relation d'ordre (j'utilise le mot "fibre" assez ingénuement ici, il y a peut-être un vocabulaire). Par exemple un ensemble ordonné qui a un plus petit(ou un plus grand) élément n'aurait qu'une seule fibre, un ensemble qui aurait plusieurs élément maximaux aurait plusieurs fibres...Je pense, en écrivant cela, aux modèles non standard de l'arithmétique (pour ceux qui ont lu un petit peu de théorie de modèles)

[serge75]

Je ne comprends pas ta formule écrite en tex.

[sept-épées]

oui, je galère avec TEX, je suis débutant. J'ai corrigé, il me semble que c'est plus lisible maintenant.

[serge75]

En gros, tu définis deux éléments en relations si on peut passer de l'un à l'autre par l'intermédiaire d'un troisième et de la relation d'ordre.
L'idée sous jacente étant si j'ai bien compris la suivante : on représente la relation sous forme d'un graphe, et tes classes seraient les orbites de ce graphe.
J'ai peur que telle quelle ta relation ne traduise pas tout à fait cette notion, ce qui créera un défaut de transitivité :
définissons sur {1,2,a,b,c} la relation suivante notée p :
p est réflexive, et 1pa ; 1pb; 2pb;2pc.
Sauf erreur de ma part, j'ai bien défini une relation d'ordre, mais ta relation R verrait a et b en relation, puis b et c en relation, sans que a et c ne le soient.
Je pense qu'il faut que tu complètes ta définition en postulant qu'on peut rejoindre deux éléments en un nombre fini d'étapes, et non plus seulement en deux étapes comme tu l'évoques.
Cordialement.

[sept-épées]

Tu as raison,

et le bon vocabulaire est sûrement celui des graphes.

L'idée est alors de décomposer le graphe de la relation en sous-graphes connexes maximaux.

Je propose donc, conformément à ta suggestion, la définition suivante :



On peut voir F comme une application de E dans l'ensemble des parties de E, et F s'étend de façon naturelle aux parties de E :



Ainsi, on peut définir par récurrence en posant :

et

Enfin, on définit

Et la relation d'équivalence est la suivante :

xRy si

Bien sûr, ça n'est pas tout à fait satisfaisant si l'on a affaire à un graphe très ramifié (j'entends grossièrement: avec plus que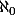 ramifications...), mais on s'en tirerait avec une induction transfinie.

[serge75]

Ceci dit, je ne vois pas dans les exemples courants de relation d'ordre 'naturelle' qui conduirait à plusieurs composantes connexes dans le graphe.
On peut en créer un artificiellement, en disant par exemple sur C :
z précède z' ssi (Re(z)=Re(z') et Im(z)<=Im(z'))
Dans ce cas, les classes s'odentifient à R, mais je vois mal l'intérêt de cette relation.
Serge

[yutor]

MERCI POUR TOUTES VOS REPONSES QUI M'AIDE A MIEUX COMPRENDRE LES NOTIONS D ESPACES QUOTIENTS ET DE RELATION D ORDRE :happy2: