Exercice sur fonction non compris

[Audiaa10]

Bonjour, pouvez vous m'aider et m'expliquer l'exercice suivant :
Le plan est rapporté à un repère (O;(vecteur)i,(vecteur)j) orthonormal, Cf est la représentation graphique de la fonction f définie sur I=[-3 , +3 ] par : f(x) = -;)x³ + 4x + 1 .

1)Etudier le sens de variation de la fonction f.
2) Ecrire une équation de la tangente T à la courbe Cf au point d'abscisse x=0
3) Déterminer, en la justifiant, la position de T par rapport à la courbe Cf.

Je vous remercie pour votre aide,
Audia.

[Arnaud-29-31]

Salut,

Tu es en quelle classe ? Quels outils tu as pour étudier les variations d'une fonction ?

[gigamesh]

bonjour,
tu es en terminale ?

Sais-tu calculer la dérivée d'une fonction ?

[Audiaa10]

Je suis en terminal L spé math, oui je sais dériver . Mais je n'ai jamais appris à calculer une tangente ainsi que la question 3.
Utiliser un tableau de signe pour la question 2 non ? :doh:

Merci

[Arnaud-29-31]

Tu as donc réussi la première question ?
Connais-tu un lien entre dérivée et tangente en un point ?

[Audiaa10]

Pour la première il suffit juste de dériver ? Si c'est le cas, oui je sais le faire . Non je ne connais pas de lien, enfin ça ne me dit rien .

[gigamesh]

LA grosse propriété à connaître sur les dérivées :

le nombre dérivé f'(a) ets le coefficient directeur de la tangente à la courbe de f au point (a;f(a)).

[Audiaa10]

Oui j'ai cette propriété dans mon cour mais comment l'appliquer à cette situation (à savoir la 2ème question) ?
Merci.

[gigamesh]

Eh bien tu cherches une équation de droite, de la forme y=mx+p.

Les renseignements dont tu disposes :
* donc la droite doit passer par le point de coordonnées (0;1)
* donc le coefficient directeur de ta tangente est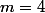

comme la droite passe par le point (0;1), on peut remplacer x par 0 et y par 1 dans l'équation, pour obtenir une égalité vraie (le principe d'une équation de droite est que l'égalité est vraie quand on remplace x et y par les coordonnées d'un point qui est sur la droite, et fausse quand on remplace x et y par des coordonnées d'un point qui n'est pas sur la droite)

on obtient

Conclusion : l'équation est y =... x + ...

Bon évidemment pour toruver p qui s'appelle "l'ordonnée à l'origine", on pouvait directement dire que (0;1) est l'intersection de la droite avec l'axe des ordonnées, donc p=1.

Une autre possibilité était d'utiliser la propriété
"l'équation de la tangente en a est y=f'(a)(x-a)+f(a)",
en remplaçant a par 0, f'(a) par 4 et f(a) par 1.

[audiiaa10]

Tout s'éclaire, je te remercie beaucoup !