Suites par récurrence TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 20:15
par skater41 » 13 Sep 2010, 20:15
Bonsoir !
J'ai un exercice à faire, et ça fait plusieurs fois que je tombe sur ce genre de chose sans jamais vraiment quoi faire ...
J'ai ma suite
)
définie par récurrence tel que
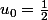
et
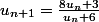
Je dois prouver que
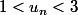
J'ai commencé ma démonstration par récurrence en calculant
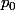
et tout ça, mais je ne sais que faire quand je dois montrer que l'encadrement est vrai pour tout n appartenant aux entiers naturels. Il faut calculer

mais je ne sais comment ... J'aimerai avoir une piste si possible, merci d'avance !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 13 Sep 2010, 20:17
par Sa Majesté » 13 Sep 2010, 20:17
Salut
Pour l'hérédité tu peux calculer
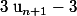
en fonction de

-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 20:21
par skater41 » 13 Sep 2010, 20:21
Pourquoi 3 ? Tu peux m'expliquer ?
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 20:23
par Teacher » 13 Sep 2010, 20:23
Déjà envois ton hypothèse de récurrence ...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 13 Sep 2010, 20:25
par Sa Majesté » 13 Sep 2010, 20:25
skater41 a écrit:Pourquoi 3 ? Tu peux m'expliquer ?
Pour montrer que
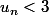
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 20:29
par skater41 » 13 Sep 2010, 20:29
Je veux que pour tout n appartenant aux entiers naturels 1<

<3
Supposons que

est vraie pour une certaine valeur de n ...
Et là je ne sais pas quoi faire
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 20:30
par skater41 » 13 Sep 2010, 20:30
Sa Majesté a écrit:Pour montrer que
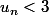
Il faudra donc que je trouve un résultat négatif ou nul ?
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 20:33
par Teacher » 13 Sep 2010, 20:33
Initialisation: D'après l'énoncé :

On suppose que la propriété est vraie au rang k (k naturel)
C'est à dire:

On montre que la propriété est vraie au rang k+1
C'est à dire : ?
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 20:36
par skater41 » 13 Sep 2010, 20:36
Teacher a écrit:Test pour le premier rang
Le rang n=0, je trouve
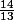
donc il est bien compris entre 1 et 3
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 20:37
par skater41 » 13 Sep 2010, 20:37
Teacher a écrit:Initialisation:

On suppose que la propriété est vraie au rang k (k naturel)
C'est à dire:

Ca aussi je l'ai fait, désolé d'avoir mal expliqué dans mon premier post ...
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 20:38
par Teacher » 13 Sep 2010, 20:38
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 20:39
par skater41 » 13 Sep 2010, 20:39
Ah oui désolé je voulais dire pour

, confusion entre l'exemple du cours et l'exercice
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 20:52
par Teacher » 13 Sep 2010, 20:52
Montre déjà que :

-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 21:18
par skater41 » 13 Sep 2010, 21:18
Pourquoi 45 ?
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 21:18
par Teacher » 13 Sep 2010, 21:18
Voilà ton brouillon


-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 21:20
par Teacher » 13 Sep 2010, 21:20
1) J'ai fais une bêtise... c'est bien

!!
-
skater41
- Membre Relatif
- Messages: 110
- Enregistré le: 05 Nov 2007, 15:52
-
 par skater41 » 13 Sep 2010, 21:25
par skater41 » 13 Sep 2010, 21:25
Mais attends je comprends pas du tout pourquoi tu me fais calculer ça, ça sort d'où ce 45 ?
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 21:29
par Teacher » 13 Sep 2010, 21:29
C'est une autre notation :

-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 13 Sep 2010, 21:33
par Teacher » 13 Sep 2010, 21:33
Teacher a écrit:C'est une autre notation :

Prouve ce que j'ai écris ci-dessus et tu comprendras puis relis là démo.
Si t'as encore des soucis, hésite pas je surveille le topic.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités