Limites

[xPsychoseN]

Bonjour. J'ai trouvé un sujet mélangeant des probabilités ainsi que des limites... Cependant je n'arrive pas a le résoudre... Et je désirerai avoir de l'aide.. Je vous donner l'énoncé :
Trouver les limites inferieures et supérieures des suites suivantes :
1. = A , = B, avec A et B deux sous ensembles de E

2. E = , = [ -1,2+1/n] , = ]-2-1/n,1]

3. E = , = ] - , ] où () est une suite de nombres réels.

Je vous remercie d'avance pour m'aider.
A bientot.

[girdav]

Ce serait un bon début de rappeler les définitions de limites supérieures et inférieures d'ensembles.
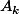
Sinon, on peut voir que être dans la limite inférieure de la suite revient à dire que l'on est dans tous les ensembles à partir d'un certain rang et être dans la limite supérieure revient à dire que l'on est dans une infinité de .
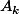
Pour la troisième question est-ce que est donné?

[xPsychoseN]

Pour la 3eme question l'énoncé est bien juste, je n'ai pas fais d'erreur...
Pour les définitions de limites sup et limites inf je les connais c'est avec les union et les intersections, mais je ne vois pas comment a partir de la je pourrais arriver a trouver les limites inf et sup... Je ne sais pas par ou commencer en fait... :triste:

[girdav]

Par exemple pour la question 1, on peut chercher pour ce que vaut .