Suites arithmétiques et géométriques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 10:43
par Dams73 » 12 Sep 2010, 10:43
Bonjour j'ai un exercice à faire mais je ne comprends pas ce qu'il faut faire voici l'énoncé
On pose Sn (Somme) = 1 + 2/3 + (2/3)² + ... + (2/3)^n
A l'aide d'une formule sommatoire, montrer que Sn < (ou égal) 3
Calculer S(indice)50 à l'aide de la calculatrice
Je sais que Sn est une somme d'une suite géométrique (Un) de raison 2/3 et de premier terme Uo = 1 je pense qu'il faut utiliser la formule de la somme de termes successif d'une suite géométrique mais je bloque dans le calcul :triste: merci d'avance pour votre aide
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 12 Sep 2010, 10:50
par Purrace » 12 Sep 2010, 10:50
donne une expression plus sympa de la formule sn
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 10:56
par Dams73 » 12 Sep 2010, 10:56
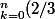 k)
?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Sep 2010, 10:59
par mehdi-128 » 12 Sep 2010, 10:59
Dams73 a écrit:Bonjour j'ai un exercice à faire mais je ne comprends pas ce qu'il faut faire voici l'énoncé
On pose Sn (Somme) = 1 + 2/3 + (2/3)² + ... + (2/3)^n
A l'aide d'une formule sommatoire, montrer que Sn < (ou égal) 3
Calculer S(indice)50 à l'aide de la calculatrice
Je sais que Sn est une somme d'une suite géométrique (Un) de raison 2/3 et de premier terme Uo = 1 je pense qu'il faut utiliser la formule de la somme de termes successif d'une suite géométrique mais je bloque dans le calcul :triste: merci d'avance pour votre aide
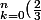^k=\frac{1-(2/3)^{n+1}}{1-2/3})
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 11:01
par Dams73 » 12 Sep 2010, 11:01
voila donc j'ai cette formule mais je ne sais pas comment calculer et ce qu'il faut trouver
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Sep 2010, 11:06
par mehdi-128 » 12 Sep 2010, 11:06
Dams73 a écrit:voila donc j'ai cette formule mais je ne sais pas comment calculer et ce qu'il faut trouver
Il suffit de montrer :
^{n+1}}{1-2/3}\leq3)
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 11:09
par Dams73 » 12 Sep 2010, 11:09
ah oui d'accord merci bon je vais calculer et je poste ma réponse
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 11:22
par Dams73 » 12 Sep 2010, 11:22
je trouve un résultat bizarre
2-(

)


3
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Sep 2010, 11:25
par mehdi-128 » 12 Sep 2010, 11:25
Dams73 a écrit:je trouve un résultat bizarre
2-(

)


3
Faux
Déja on veut démontrer :
^{n+1}}{1-2/3}\leq3)
Ce qui est équivalent à démontrer :
^{n+1}\leq1)
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 11:38
par Dams73 » 12 Sep 2010, 11:38
soit (2/3)
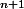

0 ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Sep 2010, 11:43
par mehdi-128 » 12 Sep 2010, 11:43
Dams73 a écrit:soit (2/3)
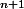

0 ?
Exactement et vu que ça c'est toujours vrai pour entier naturel tu as démontré la question
-
charif
- Membre Relatif
- Messages: 174
- Enregistré le: 30 Mar 2007, 19:32
-
 par charif » 12 Sep 2010, 11:45
par charif » 12 Sep 2010, 11:45
bj
une suite croissante de réels strictement positifs (an ajoute à la somme un réel strictement positif )
la limite de cette sommeà l'infini est 1/(1- 2/3)=3 ( car (2/3)^n+1 tend vers 0 à l'infini )
donc le Sn < 3
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 11:47
par Dams73 » 12 Sep 2010, 11:47
donc on a Sn

0 ? mais comment savoir si Sn

3 ?
-
Dams73
- Messages: 8
- Enregistré le: 10 Sep 2010, 18:36
-
 par Dams73 » 12 Sep 2010, 11:49
par Dams73 » 12 Sep 2010, 11:49
charif a écrit:bj
une suite croissante de réels strictement positifs (an ajoute à la somme un réel strictement positif )
la limite de cette sommeà l'infini est 1/(1- 2/3)=3 ( car (2/3)^n+1 tend vers 0 à l'infini )
donc le Sn < 3
Ah oui j'ai compris merci à vous deux et pour la question 2 on remplace n par 50 en utilisant la formule ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
