Bonjour à vous,
Je travaille actuellement sur un devoir, et je rencontre quelques problèmes.
(Je suis en hypokhâgne Lettres et sciences sociales )
1. De combien de façons différentes peut-on répartir sept personnes autour d'une table ronde ?
> Il ne s'agit pas d'une simple permutation, puisque cette dernière prendrait en compte des situations identiques, plusieures fois. Il faut donc fixer la première personne à une place, et organiser les autres autour, pour obtenir le nombre de possibilités d'installation des invités ? Est-ce que je me trompe ?
2. Exercice radicalement différent : Un tournoi de tennis, 2n inscris, Un est le nombre de manières d'organiser les n rencontres du premier tour.
On calcule U1, U2, U3.
Puis, il faut montrer que Un = (2n-1)(Un-1)
J'initialise une récurence, mais ne sait comment passer de Un à Un+1 pour l'hérédité ...
Je vous remercie d'avance si vous pouvez m'éclairer un peu
Bonne Journée à tous !
[HK-BL] Dénombrements
12 messages
- Page 1 sur 1
Ailin a écrit:
1. De combien de façons différentes peut-on répartir sept personnes autour d'une table ronde ?
> Il ne s'agit pas d'une simple permutation, puisque cette dernière prendrait en compte des situations identiques, plusieures fois. Il faut donc fixer la première personne à une place, et organiser les autres autour, pour obtenir le nombre de possibilités d'installation des invités ? Est-ce que je me trompe ?
C'est vrai que ce n'est pas une simple permut, mais on s'en approche!
Par exemple, pour 4 personnes les permutations:
1234, 2341, 3412 et 4321 sont les mêmes autour d'une table ronde, seul le 1er terme est changé. Donc ces 4 permuts sont 4 fois la même chose.
Transpose avec 7 personnes.
Pour ta première question, il faut d'abord que tu comptes le nombre de bijections de {1,...,7} dans {1,...} (normalement tu connais la formule), et ensuite, comme ta table est circulaire, tu dois enlever toutes celles qui sont les mêmes (je te laisse les compter également, l'indication postée par nodjim est là pour ça...)
Pour ta première question, il faut d'abord que tu comptes le nombre de bijections de {1,...,7} dans {1,...7} (normalement tu connais la formule), et ensuite, comme ta table est circulaire, tu dois enlever toutes celles qui sont les mêmes (je te laisse les compter également, l'indication postée par nodjim est là pour ça...)
Merci à vous,
C'est précisément ce que j'ai tenté de faire : Aux permutations possibles, j'ai voulu ôté celles qui étaient identiques. Et c'est là le soucis. ( D'ailleurs, Nodjim, la dernier quadruplet identique, c'est 4123, non ? ). Je ne vois pas comment caractériser ces organisations par rapport aux autres...
C'est précisément ce que j'ai tenté de faire : Aux permutations possibles, j'ai voulu ôté celles qui étaient identiques. Et c'est là le soucis. ( D'ailleurs, Nodjim, la dernier quadruplet identique, c'est 4123, non ? ). Je ne vois pas comment caractériser ces organisations par rapport aux autres...
Ailin a écrit:Merci à vous,
C'est précisément ce que j'ai tenté de faire : Aux permutations possibles, j'ai voulu ôté celles qui étaient identiques. Et c'est là le soucis. ( D'ailleurs, Nodjim, la dernier quadruplet identique, c'est 4123, non ? ). Je ne vois pas comment caractériser ces organisations par rapport aux autres...
Oui, c'est 4123.
Si tu sais calculer le nombre d'Arrangements, tu dois pouvoir t'en sortir facilement. Par exemple, pour 1234, il y a 4! arrangements, c'est à dire 4*3*2*1=24. Mais, comme dit précédemment, on doit grouper par 4 ceux qui correspondent en fait à une seule combinaison autour d'une table ronde. Au final: 24/4=6.
Si tu veux bien comprendre, établis toutes les combinaisons pour 4 personnes et identifie celles qui sont identiques. La solution ne pourra pas t'échapper.
Ailin a écrit:2. Exercice radicalement différent : Un tournoi de tennis, 2n inscris, Un est le nombre de manières d'organiser les n rencontres du premier tour.
On calcule U1, U2, U3.
Puis, il faut montrer que Un = (2n-1)(Un-1)
J'initialise une récurence, mais ne sait comment passer de Un à Un+1 pour l'hérédité ...
Celui là est plus difficile, je te recommande de partir de 2 joueurs, puis 4, puis 6 et regarder ce qui se passe. Donne un numéro par joueur, 1 à 2n, pour t'y retrouver. Bon courage.
Pour le 1. Donc, on a 7! possibilités de permutations. Mais il faut les regrouper par 7 ( Qui sont identiques, mais décalées ). On a donc 7! / 7 possibilités, soit 6! possibilités. Est-ce exact ?
Pour le 2. J'ai fait des exemples ( jusqu'à 6 ). Donc je vois ce qu'il se passe ( Les différents couples possibles, et les différents arrangements possibles ). Mais ça ne m'empêche pas de bloquer sur la récurrence. U2 est vrai ( 4 joueurs = 3 façons d'organiser le premier tour. U2=(4-1)*1. Je suppose, pour un k > 1, que Uk = (2k-1)(Uk-1). Et ne parviens pas à prouver que Uk+1=(2k-1)(Uk) ...
Merci pour l'aide =)
Pour le 2. J'ai fait des exemples ( jusqu'à 6 ). Donc je vois ce qu'il se passe ( Les différents couples possibles, et les différents arrangements possibles ). Mais ça ne m'empêche pas de bloquer sur la récurrence. U2 est vrai ( 4 joueurs = 3 façons d'organiser le premier tour. U2=(4-1)*1. Je suppose, pour un k > 1, que Uk = (2k-1)(Uk-1). Et ne parviens pas à prouver que Uk+1=(2k-1)(Uk) ...
Merci pour l'aide =)
Pour le 1. Donc, on a 7! possibilités de permutations. Mais il faut les regrouper par 7 ( Qui sont identiques, mais décalées ). On a donc 7! / 7 possibilités, soit 6! possibilités. Est-ce exact ?
Pour le 2. J'ai fait des exemples ( jusqu'à 6 ). Donc je vois ce qu'il se passe ( Les différents couples possibles, et les différents arrangements possibles ). Mais ça ne m'empêche pas de bloquer sur la récurrence. U2 est vrai ( 4 joueurs = 3 façons d'organiser le premier tour. U2=(4-1)*1. Je suppose, pour un k > 1, que Uk = (2k-1)(Uk-1). Et ne parviens pas à prouver que Uk+1=(2k-1)(Uk) ...
Merci pour l'aide =)
Pour le 2. J'ai fait des exemples ( jusqu'à 6 ). Donc je vois ce qu'il se passe ( Les différents couples possibles, et les différents arrangements possibles ). Mais ça ne m'empêche pas de bloquer sur la récurrence. U2 est vrai ( 4 joueurs = 3 façons d'organiser le premier tour. U2=(4-1)*1. Je suppose, pour un k > 1, que Uk = (2k-1)(Uk-1). Et ne parviens pas à prouver que Uk+1=(2k-1)(Uk) ...
Merci pour l'aide =)
Ailin a écrit:Pour le 1. Donc, on a 7! possibilités de permutations. Mais il faut les regrouper par 7 ( Qui sont identiques, mais décalées ). On a donc 7! / 7 possibilités, soit 6! possibilités. Est-ce exact ?
Pour le 2. J'ai fait des exemples ( jusqu'à 6 ). Donc je vois ce qu'il se passe ( Les différents couples possibles, et les différents arrangements possibles ). Mais ça ne m'empêche pas de bloquer sur la récurrence. U2 est vrai ( 4 joueurs = 3 façons d'organiser le premier tour. U2=(4-1)*1. Je suppose, pour un k > 1, que Uk = (2k-1)(Uk-1). Et ne parviens pas à prouver que Uk+1=(2k-1)(Uk) ...
Merci pour l'aide =)
C'est Ok pour le 1)
Pour le 2)
Un exemple si 8 joueurs:
Le joueur 1 peut être associé aux joueurs 2 à 8, soit 7 possibilités, 7=2n-1.
A la 1ère paire 12, on associe toutes les possibilités pour les 3 paires restantes, soit U3.
A la seconde paire 13, on associe......
et ce sont bien à chaque fois des cas différents, et on a étudié tous les cas possibles.
Donc U4=7*U3.
et Un=(2n-1)Un-1
1. Merci !
2. Ow, j'avais tenté dans cette direction, et n'étais pas parvenue au bout ! Merci pour l'aide, cette fois, je crois que j'ai saisi !
3. J'ai une dernière petite question, à la suite de la deux. On me demande de déduire de la formule précédente que pour!}{2^n * n!})
J'ai initialisé une récurrence.
Pour l'hérédité :
On suppose, pour un k > 0 que!}{2^n * n!}) .
.
Il faut montrer que!}{2^{n+1} * (n+1)!})
On a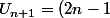(Un)) , d'après la formule prouvée précédemment.
, d'après la formule prouvée précédemment.
Soit :
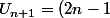\frac{(2n)!}{2^n * n!}<br />=\frac{(2n-1)(2n)!}{2^n * n!}<br />=\frac{(2(n+1)(2n-1)(2n)!}{2(n+1)*2^n * n!}<br />=\frac{(2n+2)(2n-1)(2n)!}{2^{n+1} * (n+1)!})
Or, (2n+2)(2n-1)(2n)! n'est pas égal à (2n+2)!
Sauriez vous me dire quelle est/sont ma/mes erreurs ?
2. Ow, j'avais tenté dans cette direction, et n'étais pas parvenue au bout ! Merci pour l'aide, cette fois, je crois que j'ai saisi !
3. J'ai une dernière petite question, à la suite de la deux. On me demande de déduire de la formule précédente que pour
J'ai initialisé une récurrence.
Pour l'hérédité :
On suppose, pour un k > 0 que
Il faut montrer que
On a
Soit :
Or, (2n+2)(2n-1)(2n)! n'est pas égal à (2n+2)!
Sauriez vous me dire quelle est/sont ma/mes erreurs ?
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
