Existance d'un reel verifiant f(x)=x (point fixe)

[fegore]

salut :we: :we:
j'ai besoin d'indices sur l'exo suivant

f est une fct continue positive definie sur
tel que :


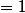
montrer que l'equation f(x)=x admet (au moine) une solution dans

[Le_chat]

C'est faux. regarde x:->x+1/(1+x).

[charif]

bs

je crois que la limite de f(x)/x devrait être égale à 0 en + l'infinie

si f(0)=0 alors il existe au moins un x

sinon f(0) est supérieur strictement à 0 ( car f positive) et f continue sur R+

or la fonction identité ( 1 ere bissectrice ) va vaincre la fonction f en + l'infinie

intuitivement elle y aura une intersection entre la fonction identité et la

fonction f pour que cette hypothèse de limite 0 soit vérifiée...

[charif]

bs

voici une preuve détaillée

si f(0)=0 c'est finie

sinon f(0) > 0 ( car f positive)
or limite de f(x)/x =0 en + l'infinie (définition de la limite) donc pour tout S > 0 il existe A >0 tq pour tout x > A f(x) <= S*x

par conséquent

pour s=1/2 il existe un A > 0 tq pour tout x > A ona f(x)<= 1/2* x < x

soit un x1 > A
posons h(x) = f(x)-x
on h (0) = f(0) - 0 = f(0) > 0 et h( x1)= f(x1)-x1 < 0 ( car x1 > A)

or h est continue( somme de 2 fonction continuesur R+) sur R+ donc d'aprés le théorème des TVI il existe un x tq

h(x)=0 d'ou il existe au moins un x tq f(x)=x