Probleme avec des suites ( ECE1 )
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
x-petro-x
- Membre Relatif
- Messages: 104
- Enregistré le: 11 Nov 2008, 14:21
-
 par x-petro-x » 11 Sep 2010, 14:05
par x-petro-x » 11 Sep 2010, 14:05
Bonjour.
Une suite d'éxo nous a été donné pour lundi et je bloque sur 2, en voici 1 :
Pour tout entier n;)1, on appelle factorielle de n, le nombre entier noté n! défini par n! = 1*2*...*n
1!=1 2!=1*2=2 ect...
On convient que 0!=1
Soit (Un)n;)0 la suite définie par Un= (2^n)/n!
1) Calculer U0 U1 U2 U3
2) Justifier que pour tout entier n;)0 : U(n+1) - Un = (2^n(1-n)) / (n-1)!
Quel est le sens de variation de la suite (Un)n;)0 ?
3) Montrer que le suite (Un)n;)0 est bornée.
Pour la 1) U0=1 U1=2 U2=2 U3=8/6. Je suis bloqué apres, je pense que c'est le n! qui me bloque. Aidez moi SVP
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2010, 14:07
par girdav » 11 Sep 2010, 14:07
Tu peux mettre en facteur
!})
quand tu calcules

.
-
x-petro-x
- Membre Relatif
- Messages: 104
- Enregistré le: 11 Nov 2008, 14:21
-
 par x-petro-x » 11 Sep 2010, 14:19
par x-petro-x » 11 Sep 2010, 14:19
J'essaie mais je vois pas... :(
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2010, 14:22
par girdav » 11 Sep 2010, 14:22
On a
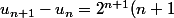!} -\fr{2^n}{n!} =\fr{2^n}{n!}\(\fr 2{n+1}-1\))
puis je te laisse continuer et rectifier la formule de ton premier message.
-
x-petro-x
- Membre Relatif
- Messages: 104
- Enregistré le: 11 Nov 2008, 14:21
-
 par x-petro-x » 11 Sep 2010, 14:28
par x-petro-x » 11 Sep 2010, 14:28
Rectifier quelle formule?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Sep 2010, 14:43
par Sa Majesté » 11 Sep 2010, 14:43
x-petro-x a écrit:2) Justifier que pour tout entier n;)0 : U(n+1) - Un = (2^n(1-n)) / (n-1)!
Ce que veut dire girdav c'est que la formule que tu as écrite est fausse
Il faut montrer que
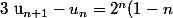}{(n+1)!})
-
x-petro-x
- Membre Relatif
- Messages: 104
- Enregistré le: 11 Nov 2008, 14:21
-
 par x-petro-x » 11 Sep 2010, 14:58
par x-petro-x » 11 Sep 2010, 14:58
Ah oui effectivement je n'avais pas vu l'erreur de signe. C'est bon j'ai reussi a trouver U(n+1)-Un. J'ai oublier une question, je dois montrer que (n+1)! = n!(n+1), et je vois pas du tout comment faire, ce qui m'a bloque pour U(n+1)-Un. Peut tu m'indiquer la bonne voie?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Sep 2010, 15:05
par Sa Majesté » 11 Sep 2010, 15:05
Ben c'est plutôt évident
(n+1)! = (n+1).n.(n-1) ... .2 x 1
n! = n.(n-1) ... .2 x 1
donc (n+1)!=(n+1).n!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
