C* dense dans la sphère de Riemann ?

[mmestre]

Bonjour,

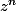
Je suis confronté à un exercice demandant de montrer qu'une fonction de dans lui-même (en l'occurence celle qui associe z à ) se prolonge de façon unique en une fonction continue de la sphère de Riemann dans elle-même.

Or la définition dont je dispose du prolongement d'une fonction par continuité suppose que l'espace topologique sur lequel la fonction est définie est dense dans l'espace de la fonction prolongée.

Ma question est donc : est-il dense dans la sphère de Riemann ?

Merci pour votre aide !

[Ben314]

Salut,
Si ce qui t'interesse est uniquement la réponse à ta question, alors c'est OUI.
Ensuite, si tu veux le "pourquoi", ben c'est assez évident : en général, on définit la sphère de Riemann comme C auquel on à ajouté un "point à l'infini" dont les voisinages sont les parties de C de complémentaire bornés.
Il est donc bien trivial que tout voisinage de l'infini contient au moins un point de C*. De même tout voisinage de 0 contient un point de C* : cela montre que C* est dense dans la sphère de Riemann.


Fait attention aussi à ta façon de rédiger les chose : Il est plus que douteux que "la définition de prolongement par continuité" demande à ce que l'espace sur lequel la fonction est défini soit dense dans l'espace sur lequel on cherche à prolonger.
A mon avis, cette condition (la densité de l'espace de départ) est plutôt une condition suffisante pour que, s'il existe, le prolongement soit unique...

[mmestre]

Bonjour Ben,

Merci beaucoup pour cette réponse détaillée.
J'aime bien l'explication de tout voisinage de l'infini (ou de zéro) qui intersecte C*..

Effectivement, la définition que j'ai dans mon livre semble passer sous silence le fait que ce n'est qu'une condition nécessaire pour avoir un prolongement unique (fait qui est néanmoins démontré rigoureusement). Ce qui arrive si l'espace de départ n'est pas dense n'est pas abordé, en tout cas pas dans ce chapitre..