Petit o..
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kromy
- Membre Naturel
- Messages: 22
- Enregistré le: 28 Nov 2009, 18:35
-
 par Kromy » 09 Sep 2010, 18:20
par Kromy » 09 Sep 2010, 18:20
Bonsoir,
Voilà, j'ai à déterminer un DL au voisinage de 0 à l'ordre 3 de 1/sin(t).
Pour cela je dis que :
1/sin(t) = 1/(t - (t^3)/6 + o(t^3))
Puis j'utilise le DL de 1/(1-x) en posant x = t^3/6 + o(t^3) d'où j'obtiens :
1/sin(t) = 1 + t^3/6 + o(t^3/6 + o(t^3)).
Est-ce que o(t^3/6 + o(t^3)) = o(t^3) ?
Si oui pouvez-vous m'expliquer svp ?
Merci d'avance.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 09 Sep 2010, 18:23
par Ericovitchi » 09 Sep 2010, 18:23
1/sin(t) = 1 + t^3/6 + o(t^3/6 + o(t^3))
Ca risque pas. 1/sin(t) tends vers l'infini quand t tends vers 0 alors que le membre de droite tends vers 1 !
-
Kromy
- Membre Naturel
- Messages: 22
- Enregistré le: 28 Nov 2009, 18:35
-
 par Kromy » 09 Sep 2010, 18:33
par Kromy » 09 Sep 2010, 18:33
Mais alors je ne comprends pas...
C'est pourtant bien la bonne méthode que j'utilise ?
Je prends le DL de 1/(1-x).
Le x vaut bien t^3/6 + o(t^3) non ?
Vaut-il uniquement t^3/6 ?
Pourquoi a-t-on :
1/(1-t^3/6+o(t^3)) = 1 + t^3/6 + o(t^3) ?
Merci.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 09 Sep 2010, 18:40
par Arnaud-29-31 » 09 Sep 2010, 18:40
Je crois qu'un t s'est transformé en 1 ... ^^
A noter que tu devras pousser le DL de sin(t) à l'ordre 5.
-
Kromy
- Membre Naturel
- Messages: 22
- Enregistré le: 28 Nov 2009, 18:35
-
 par Kromy » 09 Sep 2010, 19:09
par Kromy » 09 Sep 2010, 19:09
Non c'est bien ça...
J'ai un exo (dont j'ai le corrigé) dont l'énoncé est :
Trouver un DL à l'ordre 2 en 0 de (1/t) - 1(sin(t)).
Et le DL vaut -t/6 + o(t^2).
Et pour trouver le DL on utilise ce que j'ai écrit plus haut, qu eje ne comprends pas bien :
Pourquoi a-t-on :
1/(1-t^2/6+o(t^3)) = 1 + t^2/6 + o(t^3) ?
(ici j'ai mis t^2 au lieu de t^3 car il y a le terme 1/t de l'énoncé)

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 09 Sep 2010, 19:15
par Ericovitchi » 09 Sep 2010, 19:15
on te dit qu'il y a un t qui a sauté
quand tu es à 1/sin(t) = 1/(t - (t^3)/6 + o(t^3)) tu peux mettre un t en facteur au dénominateur et il y restera.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 09 Sep 2010, 19:24
par Arnaud-29-31 » 09 Sep 2010, 19:24
Bon, je reformule : ton expression en gras est fausse, tu as un t qui s'est transformer en 1.
Et tu verras qu'il faut pousser le DL de sin(t) à l'ordre 5 pour avoir un DL à l'ordre 3 de 1/sint
 par alavacommejetepousse » 10 Sep 2010, 07:32
par alavacommejetepousse » 10 Sep 2010, 07:32
bonjour
comme mentionné 1/sint tend vers l'infini donc n a pas de dl en 0 ...
un développement asymptotique oui

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 10 Sep 2010, 08:02
par Ericovitchi » 10 Sep 2010, 08:02
Et il faut que tu trouve ça :
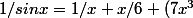/360+(31 x^5)/15120+(127 x^7)/604800+(73 x^9)/3421440+O(x^10))
 par alavacommejetepousse » 10 Sep 2010, 08:22
par alavacommejetepousse » 10 Sep 2010, 08:22
ce n est pas le dl de 1/sint ... mais de 1/sint - 1/t !
commence par réduire au même dénominateur et pour avoir un dl à l'ordre 2 développe le sin au numérateur à l'ordre 4 et au dénominateur à l'ordre 3
-
mathelot
 par mathelot » 10 Sep 2010, 08:44
par mathelot » 10 Sep 2010, 08:44
alavacommejetepousse a écrit:ce n est pas le dl de 1/sint ... mais de 1/sint - 1/t !
oui,
à
})
on soustraie la singularité
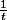
du coup
} - \frac{1}{t})
est une fonction continue, dérivable et même de classe

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
