Etude d'une suite
21 messages
- Page 1 sur 2 - 1, 2
Etude d'une suite
Bonjour,
J'essaye d'étudier la suite un+1=racine(2-un) avec u0 inconnue mais je bloque.
Ds un premier temps j'ai essayé d'étudier la fonction f(un)=un+1 qui est décroissante sur ]-infini;2] mais ensuite je n'arrive pas vraiment à continuer. Il faut probablement étudier trois cas selon les valeurs de uo?
J'essaye d'étudier la suite un+1=racine(2-un) avec u0 inconnue mais je bloque.
Ds un premier temps j'ai essayé d'étudier la fonction f(un)=un+1 qui est décroissante sur ]-infini;2] mais ensuite je n'arrive pas vraiment à continuer. Il faut probablement étudier trois cas selon les valeurs de uo?
Bonjour : :happy3:
Il s'agit d'appliquer le théorème du point fixe qui figure sur la page suivante :
http://www.les-mathematiques.net/a/m/o/node5.php3
Alors :
Tu as comme relation de recurrence :
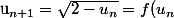 $)
avec : = \sqrt{2-x} $)
On a :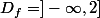 .
.
Tu verifies d'abord que : est contractante :
est contractante :
 est evidemment complet.
est evidemment complet.
Donc : la limite de est
est  tel que
tel que  est solution de l'équation :
est solution de l'équation :  = x $)
Donc, tu résouds l'équation : = x $) et tu deduis la limite de ta suite. :happy3:
et tu deduis la limite de ta suite. :happy3:
Il s'agit d'appliquer le théorème du point fixe qui figure sur la page suivante :
http://www.les-mathematiques.net/a/m/o/node5.php3
Alors :
Tu as comme relation de recurrence :
avec :
On a :
Tu verifies d'abord que :
Donc : la limite de
Donc, tu résouds l'équation :
barbu23 a écrit:Bonjour : :happy3:
Il s'agit d'appliquer le théorème du point fixe qui figure sur la page suivante :
http://www.les-mathematiques.net/a/m/o/node5.php3
Alors :
Tu as comme relation de recurrence :
avec :
On a :.
Tu verifies d'abord que :est contractante :
est evidemment complet.
Donc : la limite deest
tel que
est solution de l'équation :
Donc, tu résouds l'équation :et tu deduis la limite de ta suite. :happy3:
Oui je trouve ça et comme limite je trouve -2 et 1
AZERTY199 a écrit:C'est-à-dire?
c'est écrit ici :
http://www.les-mathematiques.net/a/m/o/node5.php3
Tu es en quelle classe ? :happy3:
Ouais, c'est vrai ! :happy3:
Donc, ce n'est pas le bon théorème à utiliser ! Il faut chercher un autre moyen que celui qu'on vient de proposer ! dommage ! :happy3:
EN plus la limite d'une suite est unique , alors que toi tu as trouvé deux qui appartiennent tous au domaine de definition ! ce n'est donc pas ce théorème qu'il faut utiliser ! :happy3:
Je reflechirai à la bonne methode ce soir et te montrer ce que j'ai fait !
A plutard ! :happy3:
Donc, ce n'est pas le bon théorème à utiliser ! Il faut chercher un autre moyen que celui qu'on vient de proposer ! dommage ! :happy3:
EN plus la limite d'une suite est unique , alors que toi tu as trouvé deux qui appartiennent tous au domaine de definition ! ce n'est donc pas ce théorème qu'il faut utiliser ! :happy3:
Je reflechirai à la bonne methode ce soir et te montrer ce que j'ai fait !
A plutard ! :happy3:
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
